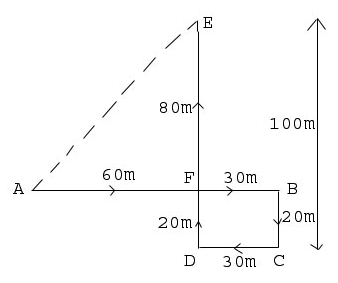
1.  A child is looking for his father. He went 90 meters in the east before turning to his right. He went 20 meters before turning to is right again to look for his father at his uncle's place 30 meters from this point. His father was not there. From there, he went 100 meters to his north before meeting his father in a street. How far did the son meet his father from starting point ?
A. 80 m
B. 90 m
C. 100 m
D. 110 m

Answer: Option C

Explanation:

Clearly, the child moves from A to B 90 metres eastwards up-to B, then turns right and moves 20 metre up to C, then turns right and moves up-to 30 metre up to D. Finally he turns right and moves up to 100 metre up-to E.

So AB = 90 metre, BF = CD = 30 metre,

So, AF = AB - BF = 60 metre

Also DE = 100 metre, DF = BC = 20 metre

So, EF = DE - DF = 80 metre

as we can see in image that triangle AFE is a right angled triangle and we are having two sides, need to calculate third one, so we can apply Pythagoras theorem here

A = AE = √(AF2 + EF2)

= √(60)2 + (80)2

= √3600 + 6400

= 100

So from starting point his father was 100 metre away.