Six dice with upper faces erased are as shows.
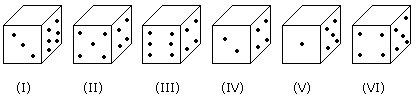
The sum of the numbers of dots on the opposite face is 7.
Page 1of 1
1
Six dice with upper faces erased are as shows.

The sum of the numbers of dots on the opposite face is 7.