| 1. |
If the even numbers of dice have odd number of dots on their top faces and odd numbered dice have even of dots on their bottom faces, then what would be the total number of dots on their top faces? |
|||||||
Answer: Option C Explanation: No. of dots on the top faces of the dice (II), (IV) and (VI) are 1, 1 and 1 respectively. No. of dots on the top faces of the dice (I), (III) and (V) are 5, 5 and 3 respectively. Required total = 5 + 5 + 3 + 1 + 1 + 1 = 16 |
Six dice with upper faces erased are as shows.
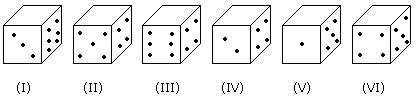
The sum of the numbers of dots on the opposite face is 7.
Post your comments here:
Name *:
Email : (optional)
Your comments will be displayed only after manual approval.