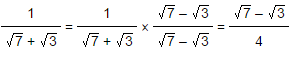Surds & Indices

Surds : which are square root and it cannot be simplified into rational numbers. But indices can be simplified.

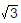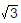For Example: (3 / 9)^(1/2) can be written as 1/ but  cannot be written in the form of fraction.

Irrational numbers which contain the radical sign ( 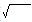) are called as surds.

Note :

1. All surds are irrational numbers.

2. All irrational numbers are not surds.

Indices: Indices refers to the power to which a number is raised. Index is used to show that a number is repeatedly multiplied by itself.

For example: a³ is a number with an index of 3 and base ‘a’. It is called as “a to the power of 3” 

---

IMPORTANT FACTS AND FORMULAE

1. Laws of Indices:

2. Surds:

Let a be rational number and n be a positive integer such that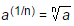
Then, 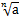is called a surd of order n.

3. Laws of Surds:

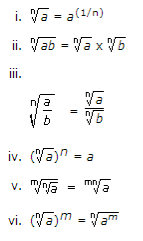
4. Expressing a number in radical form

Example: l x^(m/n) l =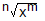 

The exponential form l x^(m/n) l is expressed in radical form as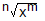 

---

Important points to Remember

1) Any number raised to the power zero is always equals to one. (Eg: x ⁰ = 1)

2) Surd 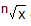can be simplified if factor of x is a perfect square.

3) If denominator in a fraction has any surds, then rationalize the denominator by multiplying both numerator and denominator by a conjugate surd.

4) Every surd is an irrational number, but every irrational number is not a surd.

5) The conjugate of (2 + 7i) is (2 – 7i)

6) Different expressions can be simplified by rationalizing the denominator and eliminating the surd.

Rationalizing the denominator:

To rationalize the denominator 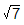multiply with its conjugate to both numerator and denominator

Example 1: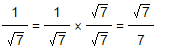

Example 2: