Percentage
All quantitative aptitude examinations will have questions based on percentage system. Most of the questions from this category are related to change of percentages or successive change of percentages.
for example "In a shop price of MacBook Air Laptop which is marked at 120,000 was discounted 20% for Christmas eve and further 30% discounted for New Year eve. What is the price of MacBook Air now?"
Here we have provided a set of basic concepts, tips and shortcuts on how to solve percentage problems easily and quickly.
The term percent means 'for every hundred' . It can be defined as follows:
"A percent is a fraction whose denominator is 100 and the numerator of the fraction is called the rate per cent." Per cent is denoted by the sign '%'.
-
Concept of Percentage:
By a certain percent, we mean that many hundredths.
Thus, x percent means x hundredths, written as x%.
To express x% as a fraction:
We have, x% = x . 100 Thus, 20% = 20 = 1 . 100 5 To express : a/b as a percent;
We have, a = 
a x 100  %.
%.b b Thus, 1 = 
1 x 100  %
%= 25%. 4 4 -
Percentage Increase/Decrease:
If the price of a commodity increases by R%, then the reduction in consumption so as not to increase the expenditure is:
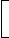
R x 100 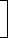 %
%(100 + R) If the price of a commodity decreases by R%, then the increase in consumption so as not to decrease the expenditure is:
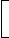
R x 100 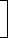 %
%(100 - R) -
Results on Population:
Let the population of a town be P now and suppose it increases at the rate of R% per annum, then:
1. Population after n years = P 
1 + R 
n 100 2. Population n years ago = P 
1 + R 
n 100 -
Results on Depreciation:
Let the present value of a machine be P. Suppose it depreciates at the rate of R% per annum. Then:
1. Value of the machine after n years :
P 
1 - R 
n 100 2. Value of the machine n years ago :
P 
1 - R 
n 100 3. If A is R% more than B, then B is less than A by:
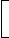
R x 100 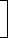 %.
%.(100 + R) 4. If A is R% less than B, then B is more than A by:
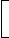
R x 100 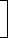 %.
%.(100 - R)
TIPS on cracking Aptitude Questions on Percentages
Tip #1 Formula for change Percentage change= {[New Value – Original Value]/ Original value} x 100%
Question: A student multiplied a number by 3/5 instead of 5/3. What is the percentage error in the calculation?
Solution:
Expected correct answer = 5/3 x Number
The new erroneous answer = 3/5 x Number
Percentage error = [3/5 – 5/3]/ 5/3 = - 64%
Question: If Sham had 24 shirts originally, by what % were his shirts reduced if he donated 4 of them?
Solution:
Percentage by which his shirts were reduced = (4 / 24) x 100%= 16.6%
Note: The most common type of questions on percentage that are encountered in any aptitude type paper is the Change Type, i.e., you will be required to calculate the percentage of change in any quantity, be it the price, population, or simply the amount of rainfall. It is imperative to remember that under all circumstances, the denominator will be the original value.
Tip #2 Questions that involve series of changes should be solved step by step
Question: By what % the new price of wardrobe has to be increased to get original value, if it was decreased by 20%?
Solution:
Let the original price be X.
Then the new price= (100 – 20) % of X= 80% of X= 0.8 X
Required raise in price= X – 0.8X= 0.2X
Percentage change in price= (0.2X / 0.8X) x 100%= 25%
Question: Ram buys good worth Rs.500. He gets a rebate of 6% on it. After getting the rebate he pays sales tax @ 10%. Find the amount he will have to pay for the goods.
Solution:
Price after rebate= 94% of Rs.500 = 0.94 x 500
Sales tax= 10% of rebated price.
Final price= 110% of price after rebate= 1.1 x 0.94 x 500 = Rs.517
Notes: Let the price of an item be first reduced by the X%, then increased by y% and then finally increased by another y%. In order to solve the problem, first consider the initial price to be P. Then calculate the first discounted price. Let it be Q. Calculate the raised price by operating upon Q. Calling this new price to be RR, calculate the final price by raising R by y%.