Syllogism
Syllogism is a Greek word, which means inference or deduction. Syllogism is a logical argument where a quantified statement of a specific form (the conclusion) is inferred from two or more quantified statements.
Few Important things to Remember
In this section, questions are based on some statements and their conclusions and you are required to identify the correct conclusion(s). You are not supposed to apply extra information except from the information given in statements, while drawing the conclusion.
Important Terms Used in Syllogism
Components of Proposition
A proposition, also known as a premise, is a grammatical sentence which comprises a subject, a predicate and a copula.
e.g.
• Quantifier The word 'All', 'No' and 'Some' are called quantifier as they specify a quantity.
• Subject (S) A subject is that part of a proposition about which something is said.
• Predicate (P) A predicate is that part of a proposition which is affirmed detail about the subject.
• Copula (C) A copula is that part of a proposition which says about the relation between the subject and the predicate.
Term
To find a logical deduction from two statements there should be three terms present. Those three terms are
- Major term It is the predicate of the conclusion and is denoted by 'P' (for predicate).
- Minor term It is the subject of the conclusion and is denoted by 'S' (for subject).
- Middle term It is the term common to both the statements and is denoted by 'M' (for middle).
Note: The middle term should not appear in the conclusion
e.g. Statements
All ships are buses.
All cars are ships.
Conclusion All cars are buses.
Here, 'buses' is the predicate of the conclusion.
Therefore, it is major term, P. 'Cars' is the subject of the conclusion. Therefore, it is the minor term, S. 'Ships' is the term common to both the statements. Therefore, it is the middle term, M.
Major and Minor Statements
The 'major statement' is that in which the middle term is the subject and the 'minor statement' is that in which the middle term is the predicate.
e.g. Statements
All dogs are cats.
All cats are white.
Here, the middle term 'cats' is the subject of second statement.
So, it is the major statement and the middle term, 'cats' is the predicate of first statement. So, it is the minor statement.
Classification of Propositions
Propositions have been classified on the basis of quality and quantity of the propositions. Quality denotes whether the proposition is affirmative or negative in nature. Quantity denotes whether the proposition is universal or particular.
Types of proposition can be understood by the following diagram
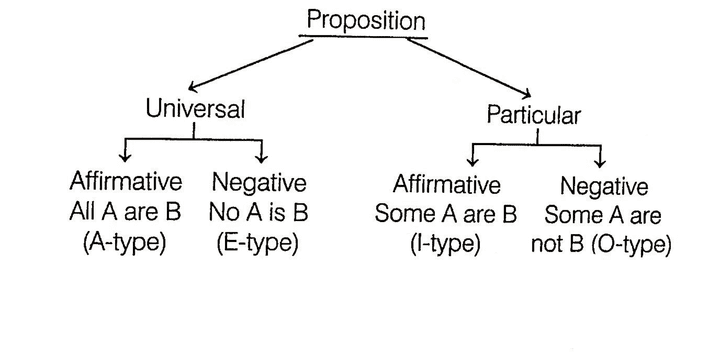
| Symbols | Proposition | Quantity | Quality |
|---|---|---|---|
| A | All A are B | Universal | Affirmative |
| E | No A is B | Universal | Negative |
| I | Some A are B | Particular | Affirmative |
| O | Some A are not B | Particular | Negative |
The four-fold proposition can be summarised as below
To draw valid inferences from the statements, the candidate is required to have a clear understanding of A, E, I, O relationships.
Venn Diagram Representation of Four Propositions
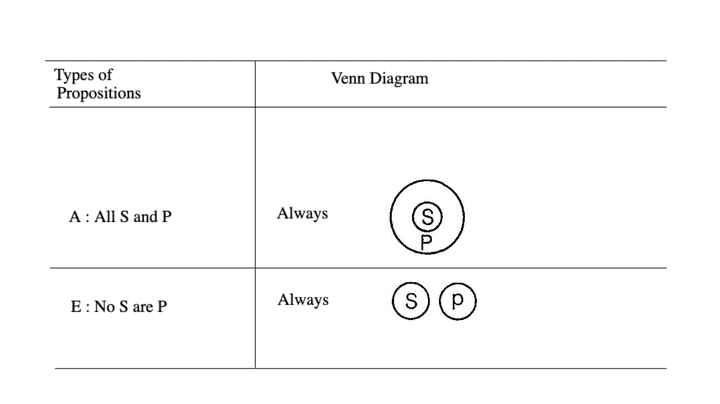
Inference
Inference is a logical conclusion derived from premises or statements known or assumed to be true.
Types of Inference
There are two types of inferences (conclusions), which are as given below
- Immediate Inference
- Mediate Inference
1. Immediate Inference
When an inference is drawn from a single statement, then it is known as 'immediate inference'.
e.g. Statement All books are pages.
Conclusion Some pages are books.
In the above example, conclusion is drawn from a single statement and does not require the second statement to be referred. Hence, the inference is called an immediate inference.
Method to Draw Immediate Inference
There are various methods to draw immediate inferences like conversion, observation, contraposition, etc., but we are required to study only following two given methods.
(i) Implications While drawing a conclusion through implication, subject remains the subject and predicate remains the predicate.
e.g. All boys are good.
Here, it is clear that if all boys are good, then some boys will definitely be good because some is a part of all.
e.g. No bags are roses.
Here, it is clear that if no bags are roses, then certainly some bags are not roses.
In the above cases, subject remains the subject and predicate remains the predicate.
Immediate inference through implication can be presented as
| Types of Propositions | Types of Inferences |
|---|---|
| A | I |
| E | O |
| I | --- |
| O | --- |
(ii) Conversions In conversions, while drawing a conclusion, subject and predicate of a proposition are interchanged, but the quality of the proposition remains the same, i.e. the affirmative remains affirmative and the negative remains negative.
e.g.
I. Statement All lamps are mangoes.
Conclusion Some mangoes are lamps.
II. Statement No men are wise.
Conclusion No wise are men.
III. Statement Some rivers are ponds.
Conclusion Some ponds are rivers.
In above cases, subject and predicate change their positions but the quality remains same.
Conversion Table
| Types of Propositions | Gets converted into |
|---|---|
| A | I |
| E | E |
| I | I |
| O | Never gets converted |
2. Mediate Inference
In mediate inference, conclusion is drawn from two given statements
e.g. Statements All dogs are cats.
All cats are black.
Conclusion All dogs are black
In the above example, conclusion is drawn from the two statements. In other words, both the statements are required to draw the conclusion. Hence, the above conclusion is know as mediate inference.
Method to Draw Mediate Inference
Step #1: Properly align pair of propositions, i.e., the common term must be the predicate of the first proposition and the subject of the second.
Let us consider the following pair of statements.
Priority order The priority should be given while aligning. According to the following rule.
i.e. important for conversion should be given first to I-type statement, then to E-type statement and finally to A-type statement.
Step #2: After having aligned statements, if required, inference can be drawn using the table as given below
| Types of I statement | Types of II statement | Types of Inference |
|---|---|---|
| A + | A = | A |
| A + | E = | E |
| E + | A = | O* |
| E + | I = | O* |
| I + | A = | I |
| I + | E = | O |
The conclusion will follow the pattern in such a way that subject of the first statement is the subject of the inference and predicate of second statement is the predicate of the inference except the case O* as shown in the table.
Where conclusion will follow the reverse pattern, i.e. subject of the first statement will be the predicate of inference and predicate of the second statement will be the subject of the inference. The given table shows the combination of statements which produce definite and valid results. All other combinations will not produce definite inferences.
Complementary Pair of Conclusions
('Either or ' Situation)
In drawing mediate inference from given statements students are required to be more attentive to select complementary pair of conclusions, where neither of the conclusions is definitely true but a combination of both makes a complementary pair.
Let us consider the example
Statements
Some cars are scooters.
Some scooters are buses.
Conclusions
I. Some cars are buses.
II. No cars are buses.
Solution : Both the statements are properly aligned, therefore fulfil the first requirement but both the statements are of I-type and as per table for immediate inference, a combination I + I does not produce any valid mediate inference. Hence, no mediate inference can be drawn.
It is important to note here, that conclusion I, 'Some cars are buses' is not valid, because there is a possibility of 'No cars are buses' , likewise conclusion II, 'No cars are buses' is invalid because there is a possibility of 'Some cars are buses'. In other words, both the conclusions are invalid individually. However, we can say that either of conclusion I or II is true. Hence, both the conclusions make a complementary pair of conclusions.
A complementary pair of conclusions must follow the following the conditions:
I. Both of them must have the same subject and the same predicate.
II. They are anyone of three types of pairs.
(i) I-O type (ii) A-O type (iii) I-E type
Note Here, we have already discussed the A, E, I and O types of the statements.
Venn Diagram Representation
Statements Some cars are scooters. Some scooters are buses.
Here, we can draw all possible cases as given below.
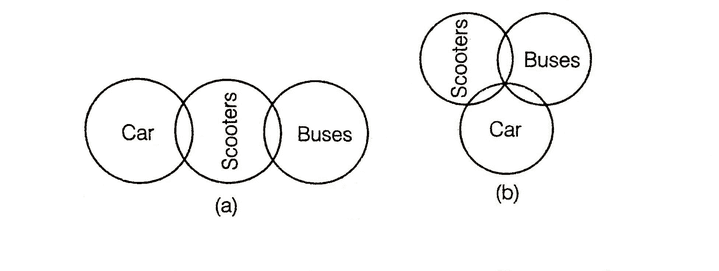
Here, using both diagrammatical representation we can conclude either 'some cars are buses' or 'No cars are buses'. Hence, at least one of the conclusions must be true.
Possibility Cases in Syllogism and Solving them using Venn Diagrams
In syllogism, when there is no exact conclusion for the given statements, then possibility case arises.
If conclusion is false is one diagram and true in another diagram, then the conclusion is deduced as partially true. In this case, partially true is considered as true.
Statements : Some walls are roads.
All roads are follows.
Conclusions :
I. All roads being walls is a possibility.
II. All walls being floors is a possibility.
Solution : All possible diagrams are as follows
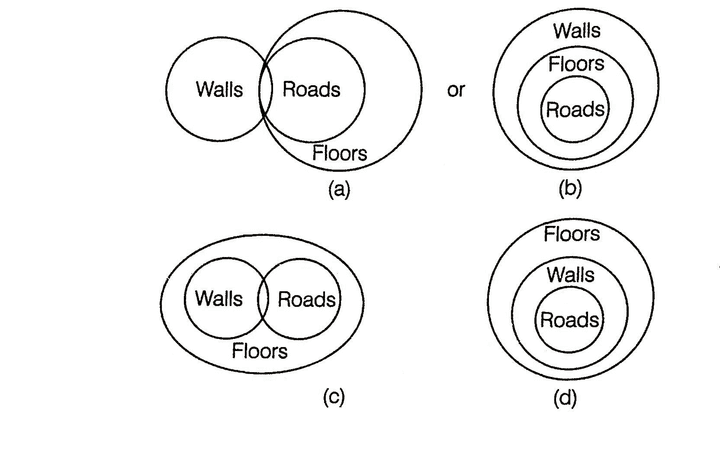
Here, the Conclusion I, i.e. 'All roads being walls is a possibility', is true in the diagrams (b) and (d).
And, the Conclusion II, i.e. 'All walls being floors is a possibility', is true in the diagrams (c) and (d).
Hence, both the conclusion follow.
Rules for Deduction
There are some rules, which are extremely helpful in deciding the conclusion whether it follows or not. They are given below
Rule #1: If one statement is negative, then the conclusion must be negative.
e.g. Statements : All books are rivers.
No river is big.
Conclusions :
I. No book is big.
II. All books are big.
Since, one statement is negative, the conclusion must be negative. Thus, Conclusion II cannot follow, only Conclusion I follows.
Alternative Method
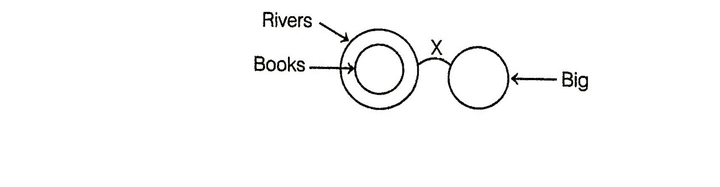
So, it is clear that rivers are not big, so no book is big. So, only Conclusion I is true.
Rule #2: If one statement is particular, then the conclusion must be particular.
e.g. Statements : Some men are wise.
All wise are doctors.
Conclusions :
I. Some men are doctors.
II. All doctors are wise.
Conclusion II cannot follow from the given statements because if one statement is particular, then the conclusion must be particular.
Therefore, Conclusion I follows.
Alternate Method
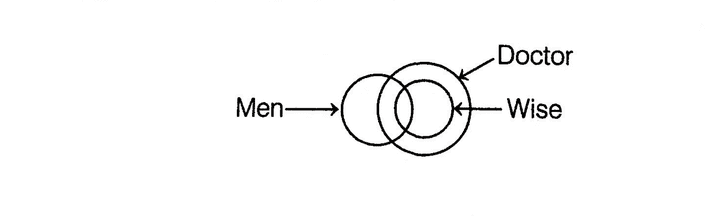
Clearly, Conclusion I follows.
Rule #3: If both the statements are affirmative, then the conclusion must be affirmative.
e.g. Statements : All books are schools.
All schools are papers.
Conclusions :
I. All books are papers.
II. Some schools are not books.
Conclusion II cannot follow, since both the statements are affirmative and so the conclusion should be affirmative. Thus, only Conclusion I follows.
Alternate Method
So, it is clear that all books are papers.
Hence, only Conclusion I follows.
Rule #4: If both the statements are particular, then no conclusion follows.
e.g. Statements : Some pens are bags.
Some bags are dogs.
Conclusions :
I. All pens are dogs.
II. Some dogs are pens.
Here, both the statements are particular.
Therefore, no conclusion follows.
Alternate Method
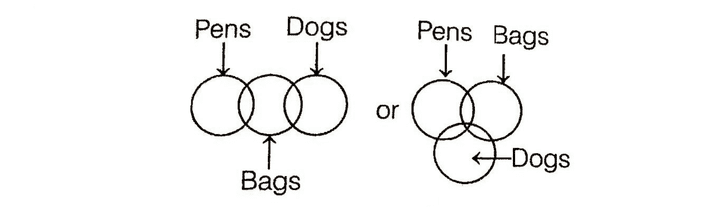
Here, we cannot find a definite conclusion.
Rule #5: If both the statements are negative, then no conclusion follows.
e.g. Statements : No man is woman.
No woman is apple.
Conclusions :
I. No man is apple.
II. Some apples are woman.
Here, both the statements are negative.
Therefore, no conclusion follows.
Alternate Method
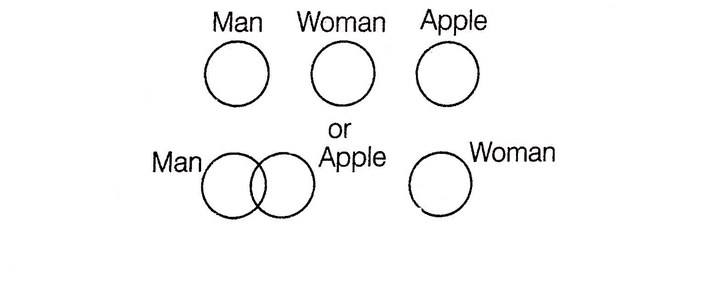
Here, we cannot find a definite conclusion.
Rule #6: If major statement is affirmative, then the conclusion must be particular.
e.g. Statements : All animals are rats.
Some dogs are animals.
Conclusions :
I. Some dogs are rats.
II. All rats are dogs.
Here, the first statement contains the middle term 'animals' as the subject and is thus, the major statement and is also affirmative. So, the conclusion must be particular. Therefore, Conclusion II cannot follow. Only Conclusion I follows.
Alternate Method
So, it is clear that some dogs are rats.
So, Conclusion I follows.
Rule #7: If the major statement is particular and the minor statement is negative, then no conclusion follows.
e.g. Statements : Some lions are tigers.
No cats are lions.
Conclusions :
I. No lions are tigers.
II. Some tigers are cats.
Here, the first statement contains the middle term 'lions' as the subject, so it is the major statement. The second statement contains the middle term 'lions' as the predicate, so it is the minor statement. Since, the major statement is particular and the minor statement is negative. So, no conclusion follows.
Alternate Method
Here, no conclusion follow.
Types of Questions
There are two types of questions which are generally asked in different competitive examinations.
Type #1:
Two or more Statement and Conclusions
In this type of questions, two or more statements are given followed by conclusions.
On the basis of the given statements, the correctness of conclusion is checked or conclusion follows from the statement or not.
Directions (Example Nos. 1-4) Two statements are given in each of the following questions, followed by two Conclusions I and II. You have to take the given two statements to be true even, if they seem to be at variance from commonly known facts. Read the conclusions and then decide which of the given conclusions logically follows from the two disregarding known facts.
Give Answer
(a) If only Conclusion I follows
(b) If only Conclusion II follows
(c) If neither I nor II follows
(d) If both Conclusions I and II follow
Example 1. Statements
All huts are mansions.
All mansions are temples.
Conclusions
I. Some temples are huts.
II. Some temples are mansions.
Solution (d)
Conclusion I - A + A = A
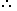All huts are mansions + All the mansions are temples
= All huts are temples ------conversion-----> Some temples are huts.
So, Conclusion I follows.
Conclusion II All mansions are temples -------conversion-----> Some temples are mansions.
So, Conclusion II follows.
Alternative Method
This shows the case of universal affirmative proposition. So,
Clearly, some temples are huts as well as some temples are mansions. So, both conclusions follow.
Example 2. Statements
Some camels are ships.
No ship is a boat.
Conclusions
I. Some ships are camels.
II. Some camels are not boats.
Solution (d) According to the question,
It is clear from diagram that both Conclusion I and II follow.
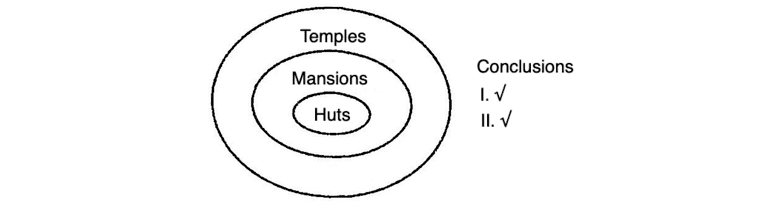
Example 3. Statements
Some chalks are dusters.
All the dusters are boards.
Conclusions
I. Some chalks are boards.
II. No dusters is a board.
Solution (a)
So, only Conclusion I follows.
Example 4. Statements
Some birds are clouds.
Horse is a bird.
Conclusions
I. Some clouds are birds.
II. Horse is not a cloud.
Solution (a) According to the question,
It is clear from diagram only Conclusion I follows.
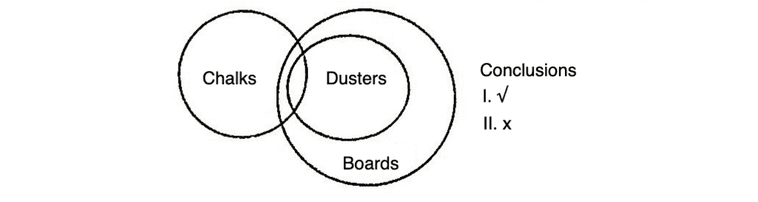
Example 5.
No parrots are black.
All crows are black.
From the above premises, which one of the following conclusions is true?
(a) Some crows are not parrots.
(b) No crows are parrots.
(c) Some parrots are not crows.
(d) No conclusion can be drawn.
Solution (b)
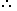No crows are parrots is correct conclusion according to the given statements.
Example 6. In the following question, three statements numbered I, II and III and four conclusions are given. Select the correct answer from the options given.
Statements
I. Some newspapers are ACs.
II. Some ACs are trees
III. All books are ACs.
Conclusions
1. Some books are newspapers.
2. All books are trees.
3. All trees are books.
4. Some books are not newspapers.
(a) Only 1 follows (b) 1 or 3 follows
(c) Either 1 or 4 follows (d) 2 and 3 follow
Solution (c) According to the question,
Conclusion 1 does not follow. Conclusion 4 also does not follow.
But these two conclusions forms a complementary pair. Therefore, either 1 or 4 follows.
Example 7. Some statements are given followed by some conclusions. You have to consider the statements to be true even, if they seem to be at variance from commonly known facts. You have to decide which of the given conclusions if any, follow from the given statements.
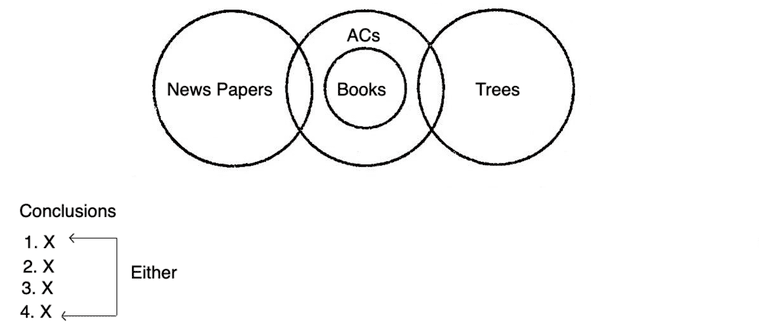
Statements Some doctors are lawyers. All teachers are lawyers. Some engineers are lawyers. All engineers are businessmen.
Conclusions
I. Some teachers are doctors.
II. Some businessmen are lawyers.
III. Some businessmen are teachers.
IV. Some lawyers are teachers.
(a) None follows (b) Only I follows
(c) Only III follows (d) II and IV follow
(e) None of these.
Solution (d) According to the question,
So, II and IV follow.
Type #2:
Find the Statements based on the given Conclusions
In this type of questions, two or more conclusions followed by four or five sets of statements are given. The candidate has to choose the correct set of statements that logically satisfies given conclusions.
Example 8 In the question below are given two conclusions followed by five set of statements. You have to choose the correct set of statements that logically satisfies given conclusions either definitely or possibly.
Assume the given statements to be true even if they seem to be at variance from commonly known facts.
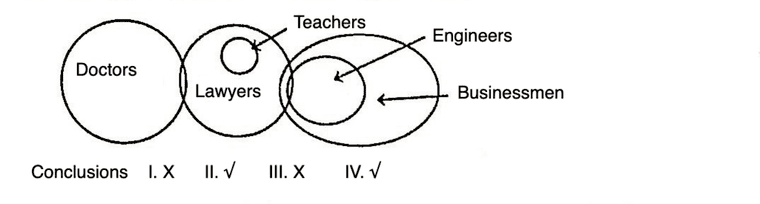
Conclusions
I. Some B is E.
II. Some J is F.
Statements
(a) All F is B. Some B is C. All C is D. All D is E.
Some E is J.
(b) Some F is B. All B is C. Some C is D. All D is E
Some E is J.
(c) Some F is E. All E is D. Some D is B. All B is C.
All C is J.
(d) All F is E. Some F is J. All J is B. Some B is D.
All D is C.
(e) None of the above
Solution (d) From option (d),
From the above diagram, it is clearly shown that some B is E and also some J is F.
LearnFrenzy provides you lots of fully solved Syllogism Questions and Answers with explanation.