Series Completion

A series is a sequence of number/alphabetical letters or both which follow a particular rule. Each element of series is called 'term'. We have to analyse the pattern find the missing term or next term to continue the pattern.

Types of Series

---

Types of Series Completion

There are mainly six types of series completion.
They are as follows

Type #1: Number Series

Number series is a form of numbers in a certain sequence, where some numbers are mistakenly put into the series of numbers and some number is missing in that series, we need to observe first and then find the accurate number to that series of numbers.

 Remember

• Even and odd numbers.

• Prime and composite numbers.

• Square and square roots of a numbers.

• Cube and cube roots of a numbers

•

---

Types of Number Series

 #1: Perfect Square Series

This type of series are based on square of a number which is in same order and one square number is missing in that given series.

Example  841, ?, 2401, 3481, 4761

Solution:

29², 39², 49², 59², 69²

 #2: Perfect Cube Series

Perfect Cube series is a arrangement of numbers in a certain order, where some number which is in same order and one cube is missing in that given series.

Example  4096, 4913, 5832, ?, 8000

Solution:

16³, 17³, 18³, 19³, 20³

#3: Mixed Number Series

Mixed number series is a arrangement of numbers in a certain order. This type of series are more than are different order which arranged in alternatively in single series or created according to any non conventional rule..

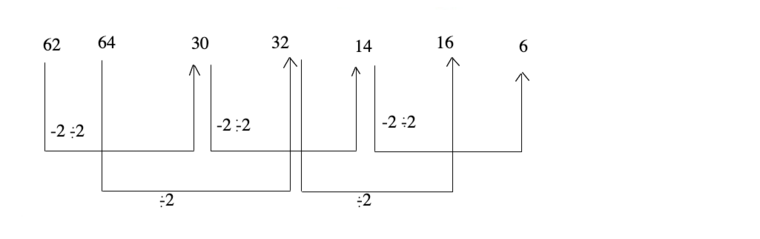
Example  62, 64, 30, 32, 14, 16, ?

Solution:

 #4: Prime Series

When numbers are a series of prime numbers.

Example  2, 3, 5, 7, 11, 13, ____, 19

Solution:

Here, the terms of the series are the prime number in order. The prime number, after 13 is 17. So, the answer to this question is 17.

 #5: Alternate Primes Series

It can be explained by below example.

Example  2, 11, 17, 23, ____, 41

Solution:

Here, the series is framed by taking the alternative prime numbers. After 23, the prime numbers are 29 and 31. So, the answer is 31.

 #6: The difference of any term from its succeeding term is constant (either increasing series or decreasing series).

Example  4, 7, 10, 13, 16, 19, ___, 25

Solution:

Here, the difference of any term from its succeeding term is 3.

#7: The difference between two consecutive terms will be either increasing or decreasing by a constant number.

Example  2, 10, 26, 50, 82, _____

Solution:

Here, the difference between two consecutive terms are

         10 -2 = 8

         26 - 10 = 16

         50 -26 = 24

         82 - 50 = 32

Here, the difference is increased by 8 (or you can say the multiples of 8). So the next difference will be 40 (32 + 8). So, the answer is 82 + 40 = 122

#8: The difference between two numbers can be multiplied by a constant number.

Example  15, 16, 19, 28, 55, _____

Solution:

Here, the difference between two numbers are

         16 - 15 = 1

         19 - 16 = 3

         28 - 19 = 9

         55 - 28 = 27

Here, the difference is multiplied by 3. So , the next difference will be 81. So the answer is 55 + 81 = 136

 #9: The difference can be multiples by number which will be increasing by a constant number.

Example  2, 3, 5, 11, 35, _____

Solution:

The difference between two number are

         3 -2 = 1

         5 - 3 = 2

        11 - 5 = 6

        35 - 11 = 24

 #10: Every third number can be the sum of the preceding two numbers.

Example  3, 5, 8, 13, 21, _____

Solution:

Here, starting from third number

         3 + 5 = 8

        5 + 8 = 13

        8 + 13 = 21

So, the answer is 13 + 21 = 34

#11: Every third number can be the product of the preceding two numbers.

Example 1, 2, 2, 4, 8, 32, _____

Solution:

Here, starting from the third number

            1 x 2 = 2

            2 x 2 = 4

           2 x 4 = 8

           4 x 8 = 32

So, the answer is 8 x 32 = 256

#12: Every succeeding term is got by multiplying the previous term by a constant number or numbers which follow a special pattern.

Example 5, 15, 45, 135, _____

Solution:

Here,

         5 x 3 = 15

        15 x 3 = 45

        45 x 3 = 135

So, the answer is 135 x 3 = 405

#13: In certain series the terms are formed by various rule (miscellaneous rules). By keen observation you have to find out the rule and the appropriate answer.

Example 4, 11, 31, 90, _____

Solution:

Terms are,

         4 x 3 - 1 = 11

         11 x 3 - 2 = 31

         31 x 3 -3 = 90

         82 - 50 = 32 

So, the answer will be 90 x 3 - 4 = 266

 #14: Triangular Pattern Series.

Sometimes the difference between consecutive terms of a series, again form a series. The differences between the consecutive terms of the new series so formed, again form a series. This pattern continues till we attain a uniform difference between the consecutive terms of the series.

Example  2, 12, 36, 80, 150, ?

Solution:

As discussed above, we may label the given series as I and them form series II to IV as shown, below:

Series - I:    2   12     36     80        150         ?

Series - II:        10      24      44      70      ?

Series - III:           14    20      26       ?

Series - IV:                     6      6

Clearly, the pattern in series III is +6.
So, missing term in series III = 26 + 6 = 32

Missing term in series II = 70 + 32 = 102

Missing term in series I = 150 + 102 = 252

Thus the missing term = 252
(i.e. 150 + 70 + 26 + 6)

---

Elementary Idea of Progressions

1. Arithmetic Progression (A.P):

The sequence of the form a, a+d, a+2d, a+3d, ....... is known as an A.P., Whose n^th term is a + (n - 1) d.
Here, 'a' is first term and 'd' is common difference.

2. Geometric Progression (G.P):

The sequence of the form a , ar, ar², ar³, ........ is known a G.P., whose n^th term is ar^n-1.

3. Find the wrong number:

In this type of questions, a series of numbers is given which follow a certain pattern and one its term does not fit into the series. The candidate is required to identify the pattern involved in the formation of series and then find out that number which does not follow the specific pattern of the series. The particular number is the wrong term in the series.

Example  One number is wrong in the following series. Find out this wrong number.

1, 5, 9, 15, 25, 37, 49

Solution:

The pattern is as follows

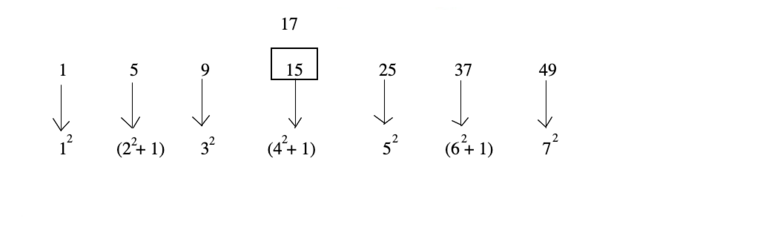
Hence number 15 is wrong and should be replaced by 17.

---

Type #2: Alphabet Series

A series that is made by only alphabetic letters.

In this type, letters of English alphabet are arranged in particular pattern like reverse order of letters, skipping of letters, position of letters in alphabetical order etc.

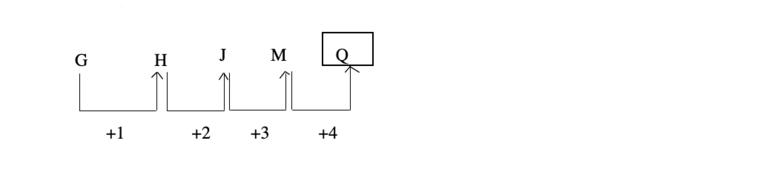
Example  G, H, J, M, ?

Solution:

 Shortcut Approach

• Remember all the alphabets and their place number.

Sometimes a word or a sentence is coded by changing the position of English alphabet letters according to a definite pattern, so it is necessary to remember the positions of all the letters in English alphabetical order, both in forward and backward order.

• Methods to Remember the Position of Letter in English Alphabet 

Some methods/techniques are given below to remember the position of English alphabets in forward or backward order.

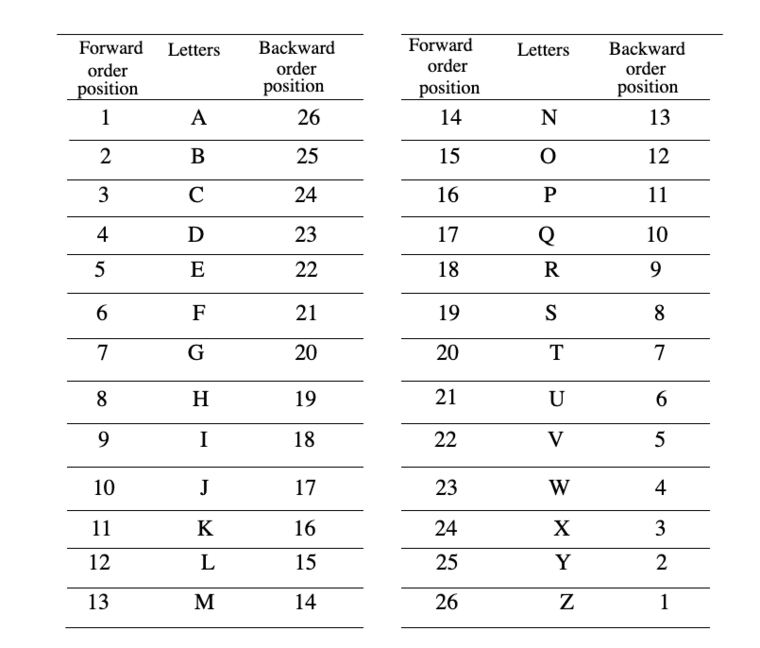
1. By using EJOTY and CFILORUX formulae, we can easily remember the position of letters of English alphabet in forward order.

Intervals like :

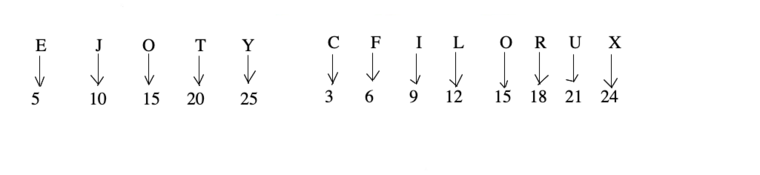
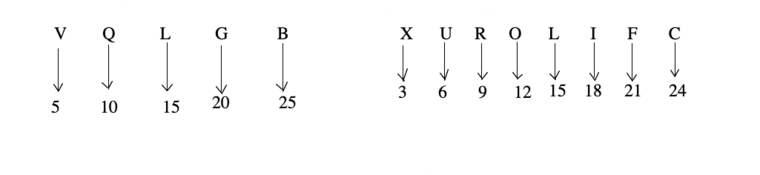
2. By using V Q L G B and X U R O L I F C, we can easily remember the position of letters of English alphabet in reverse order.

Intervals like :

---

Type #3: Alpha Numeric Series

These kind of problems used both mathematical operation and position of letters in the alphabet in forward backward order.

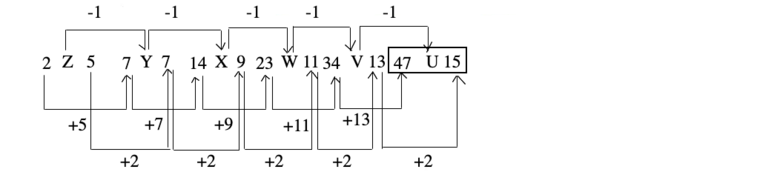
Example  2 Z 5, 7 Y 7, 14 X 9, 23 W 11, 34 V 13, ?

Solution:

---

Type #4: Mixed Series

A series formed with the combination of more than one series.

Example  A, Z, C, X, E, ?

Solution:

There are two interwoven series.

Hence, the missing term is V.

Example  Z, L, X, J, V, H, T, F, _____, _____

Solution:

The given sequence consists of two series.

(i)  Z, X, V, T, _____

(ii) L, J, H, F, _____.

Both consisting of alternate letters in the reverse order.

Next term of (i)  series = R, and
     Next term of (ii) series = D

Reverse Order Repetition Series

In such series, first part is written in reverse order of the second part of the series.

Example  R, A, M, S, H, H, S, E, M, A, ?

Solution:

Hence, the missing term is R.

Series Having Group of Letters as Its Elements

In such series, each element consists of group of letters instead of a single letter.

Example  LDP, DPL, PLD, ?

Solution: Pattern of the series as shown below

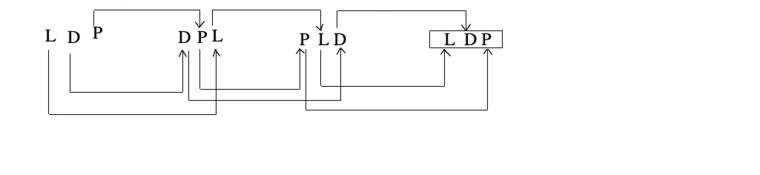
Hence, the missing term is LDP.

---

Type #5: Continuous Pattern Series

It is a series of small/capita; letters that follow a certain pattern like repetition of letters.

In this type, a series of small/capital letters are given which follow a particular pattern. However, some letters are missing from the series. The series follows a specific pattern and candidates are required to find the letters which should come in place of the blank space or question marks.

Example  The following question is based on the letter series. In each of these series, some of the letters are missing. Select the correct alternative.

b a a b - a b a - b b a - -

Solution: Pattern of the series are shown below

b a a b b a/ b a a b b a /b a

---

Type #6: Correspondence Series

This type of series consists of three sequence with three different elements (usually capital letters, digits and small letters). On the basis of the similarity in position in the three sequences, a capital letter is found to correspond with a unique digit and a unique small letter, whenever it occurs. The candidate is required to trace out this correspondence and accordingly choose the elements to be filled in at the desired places.

Example  Which of the following terms follows the trend of the given list?

C B - - D - A B C C B
- - 1 2 4 3 - - ? ? ? ?
a - a b - c - b - - - -

Solution:

Comparing the positions of the capital letters, numbers, and small letters, we find a corresponds to c and 1 correspond to a. So, a and 1 correspond to c. b corresponds to A and 2 corresponds to b. So, b and 2 corresponds to A. Also, 4 corresponds to D. Therefore, the remaining number i.e. 3 corresponds to B.

Hence, BCCB corresponds to 3113.