Matrix Coding
Matrix is a set of elements laid out in tabular form (in rows and columns).
Matrix coding is a method to represent the letters of English alphabet by two digits.
One digit is represented by the corresponding row and the other digit is represented by the corresponding column.
The questions based on matrix coding consist of two matrices i.e. Matrix I and Matrix II. Matrix I has five columns and five rows marked from 0 to 4. Five letters appear in each column and row but different in order. Matrix II has five columns and five rows marked from 5 to 9.
Five letters appear in different order in each column and row.
Candidates are required to find the assigned number to the letters of given word from the given matrices and select the group of numbers which accompanies the letter in the right format.
Let us discuss some examples to understand matrix coding.
Directions (Example Nos. 1-2)Red the following information carefully and answer the questions that follow.
In the following questions, a word is represented by only one set of numbers as given in any one of the alternatives. The sets of numbers given in the alternatives are represented by two classes of alphabets as in two Matrices given below.
The columns and rows of matrix I are numbered from 0 to 4 and that of Matrix II are numbered from 5 to 9. A letter from these matrices can be represented first by its row and next by its column.
e.g. 'M' can be represent by 01, (Row, Column) 20, (Row, Column) etc., in the same way 'T' can be represented by 57, 85 etc. Similarly, you have to identify the set for the word given in each question.
Example 1. LANE

Solutions:
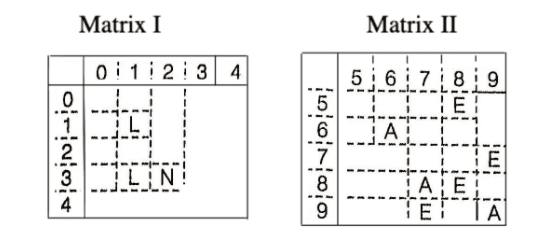
Here, taking the row and column number of each letter, we have
L = 11, 31
A = 66, 87, 99
N = 32
E = 58, 79, 88, 97
Now, taking each option and comparing them with above values, we get
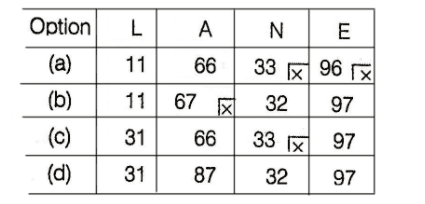
Hence, only option (d) contains all the correct values.
Example 2. A I R S

(a) 43, 55, 86, 95 (b) 12, 76, 99, 78
(c) 00, 68, 78, 88 (d) 24, 69, 56, 78
Solutions:
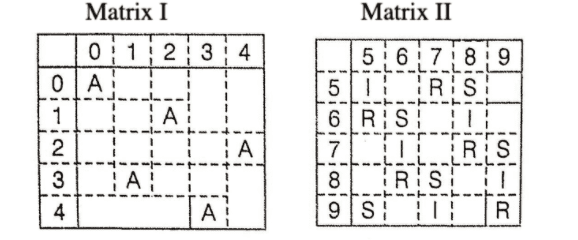
Here, taking the row and column number of each letter, we have
A = 00, 12, 24, 31, 43
I = 55, 68, 76, 89, 97
R = 57, 65, 78, 86, 99
S = 58, 66, 79, 87, 95
Now, taking each option and comparing them with above values, we get

Hence, only option (a), contains all the correct values.