Mathematical Operations

Mathematical operations are basically the simplification of an expression containing numbers and different Mathematical operations.

In this section, we deal with questions having four fundamental Mathematical operations - addition (+), subtracting (-), multiplication (x) and division (÷) and also statements such as 'less than (<)', 'greater than (>)', 'equal to (=)', 'not equal to (≠)', etc.

All these operations are represented by symbols, different from usual ones. The candidate is required to substitute the real signs in place of artificial symbols to solve the questions.

We need to follow the VBODMAS rule for simplification of Mathematical operations. This rule gives us the correct order, in which various operations regarding simplification are to be performed. Order of various operations is as same as the order of letters in the 'VBODMAS'.

mathematical-operations-verbal-reasoning-introduction---mathematical-operations-problems

Types of Questions

There are four types of questions based on mathematical operations which are usually asked in various competitive examinations

Type #1:
Problem Solving by Substitution

In this type of questions, you have substitutes for various mathematical symbols or numerals followed by a questions involving calculation of an expression or choosing the correct/incorrect equation.

Example: 1 If + means ÷, - means x, x means +, ÷ means -, then give the value for 45 + 9 - 3 x 15 ÷ 2

(a) 40 (b) 36

Solution (d) Given, 45 + 9 - 3 x 15 ÷ 2

Replacing the proper signs in the given expression,
we have 45 ÷ 9 x 3 + 15 - 2

Using VBODMAS rule,
5 x 3 + 15 - 2 = 15 + 15 - 2 = 30 - 2 = 28

Example: 2 If 'K' means 'minus', 'L' means 'divided by', 'M' means 'plus' and 'D' means 'multiplied by', then
117 L 3 K 5 M 12 D 8 = ?

(a) 150 (b) 125

Solution (c) Given, 117 L 3 K 5 M 12 D 8 = ?

Now, change the alphabet into the signs,

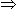? = 117 ÷ 3 - 5 + 12 x 8

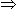? =	117	- 5 + 12 x 8
	3

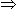? = 39 - 5 + 96

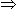? = 135 - 5 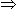? = 130

Example: 3 If '-' stands for '+', '+' stands for 'x', 'x' stands for '-', then which one of the following is not correct?

(a) 22 + 7 - 3 x 9 = 148 (b) 33 x 5 - 10 + 20 = 228

Solution (c)

From option (a),

LHS = 22 + 7 - 3 x 9 = 22 x 7 + 3 - 9
= 154 + 3 - 9 = 157 - 9 = 148 = RHS

From option (b),

LHS = 33 x 5 - 10 + 20 = 33 -5 + 10 x 20
= 33 - 5 + 200 = 233 - 5 =228 = RHS

From option (c),

LHS = 7 + 28 - 3 x 52 = 7 x 28 + 3 -52
= 196 + 3 - 52 = 199 -52
= 147 ≠ 127 (RHS)

From option (d),

LHS = 44 - 9 + 6 x 11 = 44 + 9 x 6 -11
= 44 + 54 - 11 = 98 - 11 = 87 = RHS
Hence, equation in option (c) is not correct.

Type #2:
Interchanging the Signs and Numbers

In this type of questions, certain signs or numbers interchange among each other. The candidate is required to change the given signs or numbers with each other and select the equation which is correct from the given alternatives.

It can also be asked to find the correct pair of signs and numbers to be interchanged from the alternatives to make the given equation correct.

Example: 4 If signs '+' and '-' and numbers 4 and 8 interchange between each other, then which one of the following four equations would be correct?

(a) 4 - 8 + 12 = 0 (b) 8 - 4 ÷ 12 = 8

Solution (a) Given, 4 - 8 + 12 = 0

On interchanging signs '+' and '-' and number 4 and 8 in option (a), we get
8 + 4 - 12 = 0 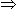12 -12 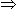= 0 0 = 0

Example: 5 Which one of the four interchanges in signs and numbers would make the given equation correct?

6 x 4 + 2 = 16

(a) + and x, 2 and 4 (b) + and x, 4 and 6

Solution (b) Given, 6 x 4 + 2 = 16

On interchanging signs '+' and 'x' and number 4 and 6 in option (b), we get
4 + 6 x 2 = 4 + 12 = 16

Type #3:
Miscellaneous Patterns

In this type, questions are based on balancing the equation by replacing the actual mathematical signs with some other signs and tricks.

Example: 6 In the following equation has to be balance, then the signs of which of the following options will be used?

24 6 12 16 = 0

(a) ÷, + and - (b) -, ÷ and +

Solution (a)

From option (a), 24 ÷ 6 + 12 - 16 = 0

LHS = 24/6 + 12 - 16
= 4 + 12 - 16 = 16 -16 = 0

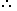LHS = RHS

Example: 7 If 5 x 4 = 15, 7 x 8 = 49 and 6 x 5 = 24, then 8 x 4 is equal to

(a) 24 (b) 26 (c) 28 (d) 30

Solution (a)

As, 5 x 4 = 5 x (4 -1) = 5 x 3 = 15
7 x 8 = 7 x (8 - 1) = 7 x 7 = 49
and 6 x 5 = 6 x (5 - 1) = 6 x 4 = 24
Similarly, 8 x 4 = 8 x (4 - 1) = 8 x 3 = 24

Example: 8 If 64 x 52 = 17, 48 x 56 = 23 and 74 x 35 = 19, then 84 x 37 = ?

(a) 32 (b) 28 (c) 22 (d) 20

Solution (c)

As, 64 x 52

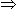(6 + 4) + (5 + 2) = 17

48 x 56

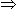(4 + 8) + (5 + 6) = 23

and 74 x 35

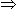(7 + 4) + (3 + 5) = 19

Similarly, 84 x 37

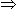(8 + 4) + (3 + 7) = 22

Type #4:
Simple and Coded Inequalities

In this type of questions, certain relationship between different sets of elements is given (in terms of 'less than', 'greater than', or 'equal to'), using either the real symbols or substituted symbols. The candidate is required to read the given statements and then choose which of the conclusions is/are definitely true.

Directions (Examples 9-11) In each of the following questions, relationship between different element is shown in the statements. These statements are followed by two conclusions.

Given Answer

(a) If only conclusion I follows
(b) If only conclusion II follows
(c) If either conclusion I or II follows
(d) If neither conclusion I nor II follows
(e) If both conclusions I and II follow

Example 9. Statements P ≥ Q = R, Q > S > T

Conclusions I. P ≥ T II. T < Q

Solution (b) On combining the two statements,
we get P ≥ Q = R > S > T

Conclusions I. P ≥ T (false)
II. T < Q (true)

So, only conclusion II follows.

Example 10. Statements A ≤ B = C,
D > C = E

Conclusions I. E ≥ A II. A < D

Solution (e) On combining the two statements,
we get A ≥ B = C = E < D

Conclusions I. E ≥ A (true)
II. D > A (true)

So, both conclusions I and II follow.

Example 11. Statements F ≥ G = H, G > J ≥ K

Conclusions I. F ≥ K II. K < H

Solution (b) On combining the two statements,
we get F ≥ G = H >J ≥ K

Conclusions I. F ≥ K (false)
II. K < H (true)

So, only conclusion II follows.

Directions (Examples 12-14) In the following questions, the symbols δ, @, ©, %, and ★ are used with the meaning as indicated below.

• 'P % Q' means 'P is neither smaller than nor equal to Q'

• 'P ★ Q' means 'P is neither greater than nor equal to Q'.

• 'P δ Q' means 'P is not greater than Q'.

• 'P @ Q' means 'P is neither greater than nor smaller than Q'.

Now, in each of the following questions assuming the given statements to be true, find which of the four conclusions I, II, III and IV given below them is/are definitely true, give your answer accordingly.

Example 12.

Conclusions I. R @ D
II. R % D
III. K ★ T
IV. M δ T

(a) Only either I or II is true
(b) III and IV are true
(c) Either I or II and III are true
(d) Either I or II and IV are true
(e) Either I or II and III and IV are true

Solution(e)

Now conclusions
I. R @ D ⇒ R = D (may be)
II. R % D ⇒ R > D (may be)
III. K ★ T ⇒ K < T (true)
IV. M δ T ⇒ M ≤ T (true)

From first two conclusions only one can be true.
Hence, either I or II and III and IV are true.

Example 13.

(a) I and II are true
(b) I, II and III are true
(c) I, III and IV are true
(d) All I, II, III and IV are true
(e) None of the above

Solution(a)

Hence, I and II are true.

Example 14.

Statements R ★ K, K % D, D @ V, V δ M

Conclusions I. R ★ D
II. V ★ R
III. D @ M
IV. M % D

(a) None is true
(b) Only III is true
(c) Only IV is true
(d) Either III or IV is true
(e) Either III or IV and II are true

Solution (d)

Here, R ★ K ⇒ R < K
K % D ⇒ K > D
D @ V ⇒ D = V
V δ M ⇒ V ≤ M
So, R < K > D = V ≤ M

Now, conclusions
I. R ★ D ⇒ R < D (false)
II. V ★ R ⇒ V < R (false)
III. D @ M ⇒ D = M (may be)
IV. M % D ⇒ M > D (may be)

Hence, either III or IV is true.

LearnFrenzy provides you lots of fully solved Mathematical Operations Questions and Answers with explanation.

Introduction

Mathematical Operations

Mathematical Operations

Types of Questions

Overview

Exercise