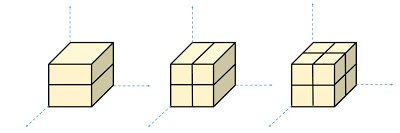
Cube and Cuboid
- 6 Faces
- 8 Vertices or corners
- 12 Edges
Now we want to cut this cube to make smaller cubes. We can do this by slicing the cube along XY, YZ and XZ planes. To get maximum number of smaller cubes with minimum number of required cuts, we should cut in equal numbers along all three axes.
Let n be the number of smaller cubes along each edge.
Then maximum cubes can be formed = n3
MIND IT !
- In a cube or a cuboid there are six faces in each.
- In a cube length, breadth and height are same while in cuboid these are different.
- In a cube the number of unit cubes = (side)3.
- In cuboid the number of unit cube = (l x b x h).
Some examples are given below:
Example-1 A cube has its sides of 5 cm in length. It is cut to make smaller cubes of size 1 cm each. Then find number of such smaller cubes formed and minimum number of cuts required.
Solution: Here smaller cube has side of 1 cm, while larger cube has its side of 5 cm. So we can have 5 such cubes on its each edges.
Hence n=5
So maximum number of such cubes formed= n3 = 53= 125
& the minimum number of cuts required to make 125 cubes = 4 + 4 + 4 = 12
For clear understanding follow these illustrations
No of Cuts: 1 Cut (Along XY Plane) 1+1=2 (XY & YZ) 1+1+1=3 (XY, YZ & XZ)From the above illustration we can deduce that:
To make (n x n x n) cubes from a larger cube,
minimum number of cuts are required = (n-1)+(n-1)+(n-1) or 3(n-1)
Example -2 Find the minimum number of cuts required to make 120 smaller cubes from a larger cube.
Solution: In such type of questions when the required number is not a perfect cube, we find the way by which this number can be formed by multiplying three integers.
Let the number to be formed is represented as: (a x b x c)
then the number of minimum cuts required = (a-1) + (b-1) + (c-1)
Here 120 can be written in multiplication of three numbers and minimum no of cuts required in all the conditions are as follows:
It is clear from the tables that minimum 12 cuts are required to make 120 cubes and we can do this by slicing 4, 5 and 6 times along its planes respectively.
You might be thinking that finding the factors is a tedious task and consumes much time. But it's not, you can get it easily by following these steps:
- Find the nearest perfect cube number & find the cube root of it.
- Check whether the given number is divisible by the cube root found in first step.
- If not divisible then check the divisibility with one above or one below of that number, again if it is not divisible then try with next number and so on.
- After division find the factors of quotient keeping in mind that both numbers are nearest to cube root calculated in first step with minimum difference.
- If possible again arrange all three numbers in such a way that their sum is minimum.
In our case we have to make 120 cubes and nearest perfect cube number 120 is 125.
We take the cube root of 125, which is 5
Now we divide 120 by 5, it gives 24 as quotient.
Factors of 24 are: ( 4 X 6 ), where both the numbers differ by 1 with 5
So we get the factor as: ( 4 x 5 x 6 ) and the minimum cuts are ( 3 + 4 + 5) = 12
Example -3 Find the minimum number of cuts required to make 50 sub cubes.
Solution: Here nearest perfect cube is 64 whose cube root is 4, But 50 is not divisible by 4,
so we take either 3 or 5 to check the divisibility.
Here 50 is divisible by 5, By dividing it by 5 we get 10 as quotient.
Now get the factor of 10, it is ( 2 x 5 )
So we get the multiples for 50 as ( 2 x 5 x 5)
& minimum cuts required is ( 1 + 4 + 4 ) = 9
Example -4 Find the minimum number of cuts required to make 920 smaller cubes.
Solution: Here nearest perfect cube is 1000 whose cube root is 10
Clearly it is divisible by 10, and we get quotient 92 by dividing 920 by 10.
Factors of 92 are ( 1 x 92 ), ( 2 x 46 ) and ( 4 x 23 )
We take factor ( 4 x 23 ) because both numbers have least difference with 10 than other pairs.
So we get the multiples as ( 4 x 10 x 23 )
But see, here we can still arrange the result to get the optimum result. We can re write it as ( 5 x 8 x 23 )
& it will require minimum cuts = 4 + 7 + 22 = 33
CUBE WITH PAINTED FACES
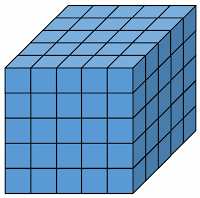
Now we are interested in cubes whose faces are painted with same color. We are taking example of ( 5 x 5 x 5 ) or 53 type of cube.
(i) How many cubes have 3 faces painted
(ii) How many cubes have 2 faces painted
(iii) How many cubes have 1 faces painted
(iv) How many cubes have none of the faces painted
(v) How many cubes are visible from outside.
Solution:
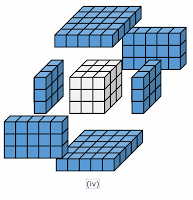
(i) All the cubes at vertices or corners have three faces painted. There are 8 such cubes.
For every cube of size 2x2x2 and above and painted in single color have 8 such cubes.
(ii) All cubes at edges except cubes at corners have two faces painted. Here every edges has 3 such cubes. So we can find the total number of such cubes are 12 x 3 = 18
(iii) All cubes at faces except cubes at edges have only one face painted. There are 3 x 3 such cubes on every face. So we can find total number of such cubes are 6 x 3 x 3 = 54
(iv) All inner cubes have none of the faces painted. These cubes doesn't lie on edges and faces. Total number of such cubes are: 3 x 3 x 3 = 27
(v) We can calculate the number of visible cubes by counting as follows
All cubes at two opposite faces: 2 ( 5 x 5 ) = 50
For other two opposite faces, Two edges are common for each face, So number of such cubes are : 2 ( 5 x 3 ) = 30
For remaining two opposite faces, every face has four 2 x 2 edges common, So number of
such cubes are : 2 ( 3 x 3 ) = 18
Total number of such cubes are: 98
Alternative: We can also calculate in shortcut way
Total Number of visible cubes = Total cubes - Interior cubes
= n3 - (n-2)3
= 125 - 27 = 98
Creating generalized formula from above example:
(i) Number of smaller cubes with 3 faces painted = 8 ( Always )
(ii) Number of smaller cubes with 2 faces painted = 12 x ( n - 2 )
(iii) Number of smaller cubes with 1 face painted = 6 x ( n - 2 )2
(iv) Number of smaller cubes with none of the face painted = ( n - 2 )3
(v) Number of visible cubes from outside = n3 - (n-2)3
TIPS on cracking Reasoning Questions on Cube and Cuboid
Tip #1: While folding a plus into a cube, the square at the longer end always forms the top of the cube and the middle square at the intersection will be the base of the cube
Question: The figure given on the left hand side in each of the following questions is folded to form a box. Choose from the alternatives (1), (2), (3) and (4) the boxes that is similar to the box formed
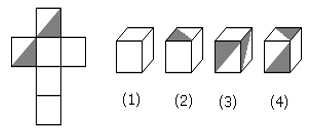
A. 1, 2 and 4 only
B. 3 and 4 only
C. 1 and 2 only
D. 1, 2 and 3 only
Solution:

The square at the longer end will form the top while the middle square will form the base. The rest 4 sides that consist of 2 unshaded squares and 2 partially shaded squares will form the lateral edges. By rotating the dice formed, we would be able to visualize (1), (2) and (4). So, the correct option will be A.
Tip #2: Draw indicative diagrams for cubes and cuboids to simplify the problem
A cuboid shaped wooden block has 4 cm length, 3 cm breadth and 5 cm height. Two sides measuring 5 cm x 4 cm are colored in red. Two faces measuring 4 cm x 3 cm are colored in blue. Two faces measuring 5 cm x 3 cm are colored in green. Now the block is divided into small cubes of side 1 cm each.
Question: How many small cubes will have two faces colored with red and green colors? Other faces of the small cube could be colored or blank.
A. 12 B. 8 C. 16 D. 20
Solution:
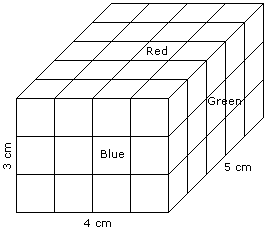
Cubes painted red and green on two sides will be along the left and right sides (5 cm length each) of the top and the bottom face. Thus, no. of such cubes = 5 x 4 = 20. Answer is D.
Question: How many small cubes will have no faces colored?
A. None B. 2 C. 4 D. 6
Solution:
The cubes that will not be part of the faces of the cuboid will have no color. Thus, no. of such cubes = 2 x 3 x 1 = 6. So the correct answer will be D.