Arithmetic Reasoning

Arithmetic reasoning involves the basic mathematical and arithmetic problems.

Arithmetic Reasoning is a part of mathematics which deals with the number sequence, mathematical operators, ratio and proportion, percentage, power and roots, sets and probability. The application of arithmetic reasoning is found in our day to day life activity like calculating the total amount of expenditure, a percentage of monthly income, to find the area of a land etc. The common arithmetic operators we use in problem are +,-,*,/, =.

MIND IT !

Arithmetic reasoning test is designed to test the ability of a candidate to solve the various Mathematical problems which are encountered in day to day life. To solve the problems on Arithmetical reasoning, a candidate should have a knowledge of concepts of arithmetic or basic Mathematics.

Examples given below, will give you a better idea about the types of questions asked in various examinations.

Example 1. If cost of 15 eggs is ₹75, then find out the cost of 4 dozens eggs.

(a) ₹240 (b) ₹300 (c) ₹150 (d) ₹185

Solution: (a) 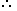Cost of 15 eggs = ₹75

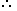Cost of 1 egg = ₹ (75/15) = ₹5

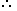Cost of 4 dozens (4 x 12 = 48) eggs = 5 x 48 = ₹240

Example 2. If a number is multiplied by three-fourth of itself, then the value thus obtained is 10800. What is that number?

(a) ₹210 (b) ₹180

Solution: (c) Let the number be x.

According to the question,

x x ( x x 3/4) = 10800

3x²/4 = 10800

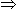x² = 10800 x 4/3 = 14400

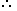x = 14400= 120

Example 3. The difference of the ages of Rohit and Axar is 12 yr. The ratio of their ages is 3 : 5.
The age of Axar is

(a) 32 yr (b) 24 yr

Solution: (d) Let present ages of Rohit and Axar be 3x and 5x, respectively.

According to the question, 5x - 3x = 12

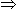2x = 12

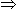x = 6

The age of Axar = 5x = 5 x 6 = 30 yr.

Example 4. There are deer and peacocks in a zoo. By counting heads they are 80. The number of their legs is 200. How many peacocks are there?

(a) 60 (b) 50

Solution: (a) Assuming deer = d and peacock = p
x4
Head ------> d + p = 80 ---------------> 4d + 4p = 320 ....(i)

Legs ------> 4d + 2p = 200 -----------> 4d + 2p = 200 ....(ii)

From subtraction Eq. (ii) from Eq. (i), we get

2p = 120 p = 120/2 = 60

Example 5. In an examination, 78% of the total students who appeared were successful. If the total number of failures was 176 and 34% got first class, then how many students got first class?

(a) 272 (b) 112 (c) 210 (d) 254

Solution: (a) Lets total students appeared in an exam = y

Then, 22% of y = 176 22/100 x y = 176

y = 176 x 100/22 = 8 x 100

y = 800

Now, number of students who got first class
= 34% of 800 = 34/100 x 800 = 34 x 8 = 272

Example 6. At the end of a business conference all the ten people present, shake hands with each other only once. How many handshakes were there altogether?

(a) 20 (b) 45 (c) 55 (d) 90

Solution: (b) Total number of handshakes = n(n-1)/2

Where, n = number of people

Total number of handshakes

= 10 (10 - 1)/2

= 10 x 9/2 = 45

Test-Taking Strategies

#1: Thoroughly read the problem

During a timed test, our inclination is to rush through each problem afraid that we’ll run out of time. Doing that in this particular part of the exam can be a recipe for disaster. Word problems can be tricky, so you have to carefully read each to discern exactly what is being asked for.

#2: Determine the question

After reading the problem, the next step is to determine exactly what the question is asking.

#3: Determine how to answer that question

In this step, you’ll need to look back at the problem and determine the best way to answer the question it is asking. This step will involve extracting the relevant facts from the problem.

#4: Create an equation or equations

Once you have determined the best way to provide the answer and have gathered the relevant facts, you need to put those facts into an equation that will give you the correct answer.

#5: Solve and review

In this final step, you will solve your equation or equations, do a quick review to make sure you have arrived at an answer that satisfies what the question is looking for and then record you answer.

LearnFrenzy provides you lots of fully solved Arithmetic Reasoning Questions and Answers with explanation.

Introduction

Arithmetic Reasoning

Arithmetic Reasoning

Test-Taking Strategies

Overview

Exercise