Volume & Surface Areas

Volume and surface area are related to solids or hollow bodies. These bodies occupy space and have usually three dimensions length, breadth and height.

Volume

Space occupied by an object is called the 'volume' of that particular object. It is always measured in cube unit like cubic meter, cubic centimetre etc.

For example If length, breadth and height of box are 9 cm, 4 cm and 2 cm respectively, then Volume of the box
= Length x breadth x Height

= 9 x 4 x 2 = 72 cm³

Surface Area

Surface area of a solid body is the area of all of its surfaces together. Surface area is measured in square unit like square meter, square centimetre etc.

For example: A cube has 6 surfaces and each surface is in a square like shape. Therefore, its surface area will be 6a² sq units, where a² is the area of each surface of the cube

---

Cracking Aptitude Questions on Volume and Surface Area

Part – I: Cube

Let the length of each edge of a cube be ‘a’. Then,

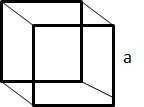
1.    Volume = a³ cubic units.

2.    Surface area = 6a² sq. units.

3.    Diagonal = a θ3 units.

Question: A large cube is formed from the material obtained by melting three smaller cubes of 3, 4 and 5 cm side. What is the ratio of the total surface areas of the smaller cubes and the large cube?

Solution:

Volume of the larger cube = Total volume of the smaller cubes

                                         = (3³ + 4³ + 5³) cm³ = 216 cm³

Side of the cube = (216)^1/3 = 6 cm

Surface area of the larger cube = 6 x 6 x 6 = 6 x 36 cm²

Total surface area of the smaller cubes = 6 x (3² + 4² + 5²) cm² = 6 x 50 cm²

Required ratio = 50 / 36 = 25:18.

Question: A 4cm cube is cut into 1 cm cubes. What is the total surface area of the new cubes?

Solution:

Number of cubes that can be formed = Total volume / Volume of each cube

                                                                  = (4 x 4 x 4) / (1 x 1 x 1) = 64.

Total surface area of all cubes = Number of cubes x Surface area of 1 cube = 64 x (6 x 1 x 1) = 384 cm²

Part – II: Cuboid

Let the length, breadth and height be ‘l’, ‘b’ and ‘h’ respectively. Then,

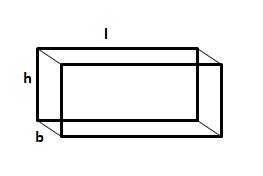
1.    Volume = (l x b x h) cubic units.

2.    Surface area = 2(lb + bh + lh) sq. units.

3.    Diagonal = ? (l² + b² + h²⁾ units.

Question: 50 men took a dip in a water tank 40 m long and 20 m broad on a religious day. If the average displacement of water by a man is 4 m³, then calculate the rise in the water level.

Solution:

Total volume of water displaced = 50 x 4 m³ = 200 m³

Change in volume of the tank occupied = length x breadth x change in height.

=>    Change in height = 200 m³ / (40 m x 20 m ) = 0.25 m = 25 cm.

Question: A cistern 6m long and 4 m wide contains water up to a depth of 1 m 25 cm. What is the surface area of the wet surface?

Solution:

Surface area of wet surface = Area occupied – Area of top surface  (since it is an open surface)

                                = Area of cuboid – Area of base

                                = 2(lb + bh + lh) – lb

                                = 2(6x4 + 4x1.25 + 6x1.25) – 6x4

                                = 2x1.25x10 + 24 = 49 m²

Part – III: Cylinder

Let radius of the base of a cylinder be ‘r’ and its height be h. Then,

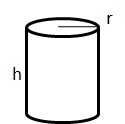
1.    Volume = ? (r²h) cubic units.

2.    Curved surface area = (2 ? rh) sq. units.

3.    Total surface area = 2 ? r(h + r) sq. units.

Question: A hollow iron pipe is 21 cm long and its external diameter is 8 cm. If the thickness of the pipe is 1 cm and iron weighs 8 g/cm³, what is the weight of the pipe?

Solution:

External radius R = 4 cm, Internal radius r = (4 – 1) cm = 3 cm

Volume of the pipe = Total solid volume – Volume of hollow part

                       = ?(R² – r²)h

                       = 22 / 7 x (4x4 – 3x3) x 21 = 462 cm³.

Mass of the pipe = density x volume

                      = 8 x 462 = 3696 gm = 3.696 kg.

Question: 66 cm³ of silver is drawn into a wire 1 mm in diameter. Find the length of the wire in meters.

Solution:

Radius of the wire r = 0.5 mm = 0.05 cm and let length = l.

Volume of the wire = 66 cm³ = ? r² l = 22 / 7 x 0.05 x 0.05 x l

=>    l = 66 x 7 / (22 x 0.05 x 0.05) = 8400 cm = 84 m.

 

Part – IV: Sphere and Hemi-Sphere

Let the radius of the sphere be r. Then,

1.    Volume = (4 / 3) ? r³ cubic units.

2.    Surface area = (4 ? r²) sq. units.

For a hemisphere of radius r, we have

1.    Volume = (2 / 3) ? r³ cubic units.

2.    Curved surface area = (2 ? r²) sq. units.

3.    Total surface area = (3 ? r²) sq. units.

Question: The volume of a spherical ball is 121000 cm³. What is the radius of the ball?

Solution:

(4 / 3) ? r³ = 121000

=>    r³ = 121000 x 3 / 4 x 7 / 22 = 28875

=>    r = (28875)^1/3 = 30.68 cm.

Question: Calvin is making a model Earth in his science class. The radius of the inner core of the model Earth is 4 cm and the radius of the entire model is 10 cm. How many times larger is the volume of the entire model than the volume of the inner core?

Solution:

Volume of core = (4 / 3) ? x 4 x 4 x 4 cm³

Volume of earth = (4 / 3) ? x 10 x 10 x 10 cm³

Volume of entire model = (1000 / 64) times the volume of the core

                              = 15.625 times the volume of the core.

Part – V: Cone

Let radius of base = r and Height = h. Then,

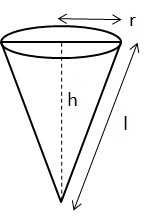
1.    Slant height, l = ?(h² + r²) units.

2.    Volume = (? r²h / 3) cubic units.

3.    Curved surface area = (? rl) sq. units.

4.    Total surface area = ?rl + ? r² sq. units.

Question: A right triangle with sides 3 cm, 4 cm and 5 cm is rotated along the side of 3 cm to form a cone. Find the volume of the cone so formed.

Solution:

From the question, we can say that r = 3 cm, h = 4 cm and l = 5 cm.

Thus, volume of the cone = ? x 3 x 3 x 4 / 3

                                   = 12 ? cm².

Question: The slant height of a right circular cone is 10 m and its height is 8 m. Find the area of its curved surface.

Solution:

Given, l = 10 m and h = 8 m.

r = ?(l² – r²) = ?(100 – 64) = 6 m

Curved surface area = ? x r x l

                         = ? x 6 x 10 = 60 ? m².