Simplification
Simplification is the very important and high marks scope section in quantitative aptitude. Aspirants must know formulas including tricks to score maximum marks in simplification section. This section at least having minimum weightage of 10 marks out of 40 marks in quantitative aptitude. In this section you can learn and practice maximum models those are frequently asked in this part.
The simplification of any mathematical expression is the process of conversion of complex expression (expression having different types of brackets enclosing different mathematical operations like addition, multiplication and division etc.) into a simple expression by performing various mathematical operations with specific rules in a sequence.
i.e., A complex arithmetical expression can be converted into a simple expression by simplification.
When you simplify any problem which in complex expression, you must follow the VBODMAS rule. Without this rule you can’t solve these type problems, even if you get answer that will be wrong according to rule. So we need to start from this rule primarily.
'VBODMAS' Rule
To simplify arithmetic expressions, which involve various operations like brackets, multiplication, addition, etc; a particular sequence of the operations has to be followed.
The operations have to be carried out in the order, in which they appear in the word VBODMAS, where different letters of the word stand for following operations.
V means Vinculum or Bar '-'
(The bar you see on top of the values X )
B means Bracket – () {} [ ]
O means Of
D means Division [/]
M means Multiplication [x]
A means Addition [+]
S means Subtraction [-]
Order of above mentioned operations is same as the order of letters in the 'VBODMAS' from left to right as
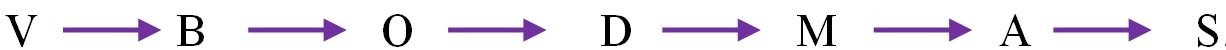
Here the above rule explains the sequence needs to be follow in simplification.
MIND IT !
Absolute value of a Real Number:
If m is a real number, then its absolute value is defined as
| |m| = |  |
m, if m > 0 |
| -m, if m < 0 |
Thus, |5| = 5 and |-5| = -(-5) = 5.