Ratio and Proportion


Ratio

When two or more similar quantities are compared, then to represent this comparison, ratios are used.

or

Ratio of two quantities is the number of times one quantity contains another quantity of same kind.

The ratio between x and y can be represented as x : y, where x is called antecedent and y is called consequent.

x/y or x : y

Eg. The ratio 5 : 9 represents 5/9 with antecedent = 5, consequent = 9.

For example There can be a ratio between 100 and 500, but there cannot be the ratio between 100 and 500 apples. Hence, the unit of quantity for the comparison of ratio should be same.

Types of Ratio


The different types of ratio are explained as under

  1. Duplicate Ratio If two numbers are in ratio, then the ratio of their squares is called duplicate ratio. If x and yare two numbers, then the duplicate ratio of x and y would be x2 : y2.

    2. Duplicate ratio of (x : y) is (x2 : y2).

    For example Duplicate ratio of 3 : 4 = 32 : 42 = 9 : 16

  2. Sub-duplicate Ratio If two numbers are in ratio, then the ratio of their square roots is called sub-duplicate ratio. If x and y are two numbers, then the sub-duplicate ratio of x and y would be (x : y)

    3. Sub-duplicate ratio of (x : y) is (x : y).

  3. Triplicate Ratio If two numbers are in ratio, then the ratio of their cubes is called triplicate ratio. If x and y are two numbers, then the triplicate ratio of x and y would be x3 : y3.

    4. Triplicate ratio of (x : y) is (x3 : y3).

    For example Triplicate ratio of 2 : 3 = 23 : 33 = 8 : 27

  4. Sub-triplicate Ratio If two numbers are in ratio, then the ratio of their cube roots is called sub-triplicate ratio. If a and b are two numbers, then the sub-triplicate ratio of a and b would be a1/3 : b1/3

    5. Sub-triplicate ratio of (a : b) is (a1/3 : b1/3).

    If a = c , then a + b = c + d .    
    b d a - b c - d

    [componendo and dividendo]

    For example Sub-triplicate ratio of 1 : 125 = (1)1/3 : (125)1/3 = 1: 5

  5. Inverse Ratio If two numbers are in ratio, then their antecedent and consequent are interchanged and the ratio obtained is called inverse ratio. If x and y are two numbers and their ratio is x : y,
    then its inverse ratio will be y : x

    6. For example Inverse ratio of 4 : 5 is 5 : 4.

  6. Compound Ratio If two or more ratios are given, then the antecedent of one is multiplied with antecedent of other and respective consequents are also multiplied with antecedent of other and respective consequents are also multiplied. If a : b, c : d and e : f are three ratios, then their compound ratio will be ace : pdf.

    7. The compounded ratio of the ratios: (a : b), (c : d), (e : f) is (ace : bdf).

    For example The compound ratio of 2 : 5, 6 : 7 and 9 : 13 = (2 x 6 x 9) / (5 x 7 x 13) = 108 / 455

MIND IT !

  1. If the antecedent is greater than the consequent, then the ratio is known as the ratio of greater inequality, such as 7 : 5.
  2. If the antecedent is less than the consequent, then the ratio is called the ratio of less inequality, such as 5 : 7.

Comparison of Ratios

We say that (a : b) > (c : d)     a > c .
b d

Rules used to compare different ratios are as follows


Rule #1: If the given ratios are a : b and c : d, then
(i) a : b > c : d, if ad > bc (ii) a : b < c : d, if ad < bc (iii) a : b = c : d, if ad = bc


Example 1: Which is grater 5/8 or 9/14 ?

sol. Let a/b = 5/8 and c/d = 9/14; 

ad = 5 x 14 = 70 and bc = 8 x 9 =72

Therefore  ad < bc

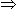  a/b < c/d = 5/8 < 9/14


Rule #2: If two ratios are given for comparison, convert each ratio in such a way that both ratios have same denominator, then compare their numerators, the fraction with greater numerator will be grater.


Example 2:Find the greater ratio between 2 : 3 and 4 : 5.

sol. (2 x 5) / (3 x 5) = 10/15 and
       (4 x 3) / (5 x 3) = 12/15

[ LCM of 2/3 and 4/5 i.e., 3 and 5 is 15]

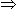12/15 > 10/15

  4 : 5 > 2 : 3


Rule #3: If two ratios are given for comparison, convert each ratio in such a way that both ratios have same numerator, then compare their denominators, the fraction with lesser denominator will be greater.


Example 3: Find the least fraction between 6/7 and 7/9.

sol. (6 x 7) / (7 x 7) = 42/49 and
       (7 x 6) / (9 x 6) = 42/54

[ LCM of 6/7 and 7/9 i.e., 6 and 7 is 42] 

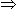 42/49 > 42/54
 6/7 : 7/9

Proportion


An equality of two ratios is called the proportion. If a/b = c/d or a : b = c : d, then we can say that a, b, c and d are in proportion and can be written as a : b :: c : d, where symbol ' :: ' represents proportion and it is read as 'a is to b' as 'c is to d'.

Here, a and d are called 'Extremes' and b and c are called as 'Means'.

Product of means = Product of extremes.

Thus, a : b :: c : d (b x c) = (a x d).

Variations


We say that x is directly proportional to y, if x = ky for some constant k and we write, x 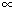y.

We say that x is inversely proportional to y, if xy = k for some constant k and

we write, x 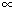1 .
y

TIPS on cracking Aptitude Questions on Ratios and Proportions


Tip #1: Express each element in the ratio as a fraction of the total for easy calculations

Question: A sum of money is to be distributed among A, B, C, D in the proportion of 2: 5: 4: 3. If C gets Rs.2000 more than D, what is B's share?

Solution:

A = 2/14 * T

B = 5/14 * T

C = 4/14 * T

D = 3/14 * T

C – D = 2000

4/14 * T – 3/14 * T = 2000

T = 28000

=> B = 5/14 * T = Rs.10000


Tip #2: You can directly perform multiplication/ division operations on ratio elements

Question: Seats for Mathematics, Physics and Biology in a school are in the ratio 5 : 7 : 8. There is a proposal to increase these seats by 40%, 50% and 75% respectively. What will be the ratio of increased seats?

Solution:

Seats Before Proposal     After Proposal
Mathematics Seats    5/20 * T     5/20 * T * 1.4
Physics Seats    7/20 * T     7/20 * T * 1.5
Biology Seats    8/20 * T     8/20 * T * 1.75

                       

Ratio after proposal   = 5/20 * T * 1.4 : 7/20 * T * 1.5 : 8/20 * T * 1.75

                                = 5/20 * 1.4 : 7/20 * 1.5 : 8/20 * 1.75    {dividing by T}

                                = 5 * 1.4 : 7 * 1.5 : 8 * 1.75    {multiplying by 20}

                                = 7 : 10.5 : 14   

                                = 2 : 3 : 4    {dividing by 3.5}

As a quick shortcut, we can also directly multiply the ratio elements to determine the new ratio.

Ratio after proposal (shortcut)  = 5 * 1.4 : 7 * 1.5 : 8 * 1.75

                                             = 2 : 3 : 4


Tip #3: Ensure that the units for the numerator and denominator match across the equation

Question: Ken can walk 40 dogs in 8 hours. How many dogs can Ken walk in 12 hours?

Solution:

We assume that the number of dogs walked and the time taken are directly proportional.

Number of dogs walked ?Time taken

Number of dogs walked = k * Time taken    (k is some constant)

Number of dogs walked / Time taken = k

40 / 8 = x / 12    where x is count of dogs walked in 12 hours

In the above equation, numerator unit is dogs walked and denominator unit is time taken. Ensure that units match to avoid errors.

=> x = 60 dogs walked