Profit and Loss
Profit and loss are the terms related to monetary transactions in trade and business. Whenever a purchased article is sold, then either profit is earned or loss is incurred.
Important Facts
Cost Price (CP) The price, at which an article is purchased, is called its cost price, abbreviated as C.P.
Selling Price (SP) The price, at which an article is sold, is called its selling prices, abbreviated as S.P.
Overhead Charges Such charges are the extra expenditures on purchased goods apart from actual cost price. Such charges include freight charges, rent, salary of employees, repairing cost on purchased articles etc.
Note : If overhead charges are not specified in the question, then they are not considered.
Profit or Gain (SP>CP) :
If S.P. is greater than C.P., the seller is said to have a profit or gain.
Loss (CP>SP) :
If S.P. is less than C.P., the seller is said to have incurred a loss.
MIND IT !
1. Profit and loss are always calculated on cost price unless otherwise stated in the question
2. If an article is sold at a certain gain (say 45%), then SP = 145% of CP
3. If an article is sold at a certain loss (say 25%), then SP = 75% of CP
Important Formulae
-
Gain = (S.P.) - (C.P.)
-
Loss = (C.P.) - (S.P.)
-
Loss or gain is always reckoned on C.P.
-
Gain Percentage: (Gain %)
Gain % = 
Gain x 100 
C.P. -
Loss Percentage: (Loss %)
Loss % = 
Loss x 100 
C.P. -
Selling Price: (S.P.)
SP = 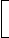
(100 + Gain %) x C.P 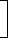
100 -
Selling Price: (S.P.)
SP = 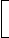
(100 - Loss %) x C.P. 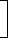
100 -
Cost Price: (C.P.)
C.P. = 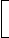
100 x S.P. 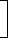
(100 + Gain %) -
Cost Price: (C.P.)
C.P. = 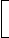
100 x S.P. 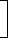
(100 - Loss %) -
If an article is sold at a gain of say 35%, then S.P. = 135% of C.P.
-
If an article is sold at a loss of say, 35% then S.P. = 65% of C.P.
-
When a person sells two similar items, one at a gain of say x%, and the other at a loss of x%, then the seller always incurs a loss given by:
Loss % = 
Common Loss and Gain % 
2 10 = 
x 
2 . 10 -
If a trader professes to sell his goods at cost price, but uses false weights, then
Gain % = 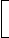
Error x 100 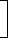 %.
%.(True Value) - (Error)
Formula for Cracking Aptitude Questions on Profit and Loss
Reduce the problem to one equation and use the formula: Selling Price = Cost Price (1 + 0.01 x profit percentage)
Question: Alfred buys an old scooter for Rs.4700 and spends Rs.800 on its repairs. If he sells the scooter for Rs.5800, what is his gain percent?
Solution:
Net C.P. = Cost + Repairs= Rs.4700 + 800= Rs.5500
S.P. = Rs.5800
Now, 5800= 5500(1+0.01p)
=> p = 300/(550x0.01)= 5.45 %
Question: By selling a Jeans for $ 432, John loses 4%. For how much should John sell it to gain 6%?
Solution:
For the first transaction, we have:
=> 432 = C.P. (1-0.04) = C.P. * 0.96 => C.P. = 432/0.96
For the second transaction, we have:
=> S.P. = C.P. (1+0.06) = (432/0.96) * 1.06
=> S.P.= $477
Note: All the problems on profit and loss can be reduced to a single step that can be solved directly using the formula S.P. =C.P. (1±0.01x), where x is the profit/loss percent. Remember that the ’+’ve sign is used when a profit is incurred and the ‘-’ve sign is used when a loss is incurred.