| 1. |
In a two-digit number, if it is known that its unit's digit exceeds its ten's digit by 2 and that the product of the given number and the sum of its digits is equal to 144, then the number is : |
|||||||
Answer: Option A Explanation: Let the ten's digit be x. Then, unit's digit = x + 2. Number = 10x + (x + 2) = 11x + 2. Sum of digits = x + (x + 2) = 2x + 2.
Hence, required number = 11x + 2 = 24. |
Post your comments here:
Name *:
Email : (optional)
Your comments will be displayed only after manual approval.
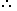 (11x + 2)(2x + 2) = 144
(11x + 2)(2x + 2) = 144 22x2 + 26x - 140 = 0
22x2 + 26x - 140 = 0