Probability
Probability means the chances of happening/occurring of an event. So, in this section we discuss about the predictability of an event to happen/occur. We usually predict about many events based on certain parameters.
For Example
(i) Getting a head or tail, when a coin is tossed
(ii) Getting a number from 1 to 6, when a die is rolled.
The better we know about the parameters related to an event better will be the accuracy of the result predicted.
Mathematically, we can say that probability of happening an event is equal to the ratio of number of favourable outcomes to number of possible outcomes.
It is represented as shown below
Probability happening of an event P
| = | Number of favourable outcomes | . |
| Total number of possible outcomes |
Important Facts & Formulae
Probability is based on observations of certain events. Probability of an event is the ratio of the number of observations of the event to the total numbers of the observations.
1. Experiment: An operation which can produce some well-defined outcomes is called an experiment.
2. Random Experiment: An experiment in which all possible outcomes are know and the exact output cannot be predicted in advance, is called a random experiment.
Examples of Performing a Random Experiment :
(i) Rolling an unbiased dice.
(ii) Tossing a fair coin.
(iii) Drawing a card from a pack of well-shuffled cards.
(iv) Picking up a ball of certain colour from a bag containing balls of different colours.
Details:
(i) Tossing of a fair coin
When we toss a coin, the outcome will be either Head (H) or Tail (T)
(ii) Throwing an unbiased die
Die is a small cube used in games. It has six faces and each of the six faces shows a different number of dots from 1 to 6. Plural of die is dice.
When a die is thrown or rolled, the outcome is the number that appears on its upper face and it is a random integer from one to six, each value being equally likely.
(iii) Drawing a card from a pack of shuffled cards
A pack or deck of playing cards has 52 cards which are divided into four categories as given below
- Spades
- Clubs
- Hearts
- Diamonds
Each of the above mentioned categories has 13 cards, 9 cards numbered from 2 to 10, an Ace, a King, a Queen and a jack
- It has 13 cards of each suit, name Spades, Clubs, Hearts and Diamonds.
- Cards of spades and clubs are black cards.
- Cards of hearts and diamonds are red cards.
- There are 4 honours of each unit.
- Kings, Queens and Jacks are called face cards
3. Sample Space: When we perform an experiment, then the set S of all possible outcomes is called the sample space.
Examples of Sample Spaces:
(i) In tossing a coin, S = {H, T}
(ii) If two coins are tossed, the S = {HH, HT, TH, TT}.
(iii) In rolling a dice, we have, S = {1, 2, 3, 4, 5, 6}.
4. Event: Any subset of a sample space is called an event.
5. Probability of Occurrence of an Event:
Let S be the sample and let E be an event.
Then, E  S.
S.
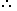 P(E) = P(E) = |
n(E) | . |
| n(S) |
6. Results on Probability:
(i) P(S) = 1
(ii) 0 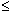 P (E)
P (E) 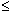 1
1
(iii) P(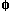 ) = 0
) = 0
(iv) For any events A and B we have : P(A 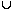 B) = P(A) + P(B) - P(A
B) = P(A) + P(B) - P(A 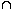 B)
B)
(v) If A denotes (not-A), then P(A) = 1 - P(A).
TIPS on cracking Aptitude Questions on Probability
Tip #1: Categorize the events as mutually dependent, independent or exclusive
Mutually Dependent Events: 2 or more events are that are such that the occurrence of one affects the occurrence of the other. The words ‘and’, ‘together’, ‘all’, etc. indicate that the events are mutually dependent.
Example: Let a card is chosen at random from a standard deck of 52 playing cards. Without replacing it, a 2nd card is chosen.
The probability of choosing any card is 1 out of 52. However, if the 1st card is not replaced, then the 2nd card is chosen from only 51 cards. Accordingly, the probability of choosing another card is 1 out of 51. Thus, these events are mutually dependent.
Mutually Independent Events: 2 or more events such that the occurrence of one does not affect the occurrence of the other. If the problem is such that after each event, the sample space is restored to its original state, then the events are mutually independent.
Example: In the above example, the 1st card that was drawn is replaced before drawing the 2nd card. The probability of choosing any card is 1 out of 52. Now, the 1st card is replaced, then the 2nd card is chosen from 52 cards again. Accordingly, the probability of choosing another card is 1 out of 52. Thus, these events are mutually independent.
Mutually Exclusive Events: 2 or more events that cannot happen simultaneously. The indicative words are ‘or’, ‘at most’, ‘at least’, etc.
Example: The events “running forward” and “running backwards” are mutually exclusive. Similarly, you can’t toss a coin and get both a heads and tails at the same time, so “tossing a heads” and “tossing a tails” are mutually exclusive.
Tip #2: Probability of occurrence of mutually exclusive events is the sum of their individual probabilities
Question: Three unbiased coins are tossed. What is the probability of getting at most two heads?
Solution:
Probability of getting at most 2 heads = Probability of getting no head + Probability of getting 1 head + Probability of getting 2 heads
Probability of getting no heads = Probability of getting all tails = ( ½ )( ½ )( ½ ) = 1/8
Probability of getting 1 head = C(3,1)( ½ )( ½ )( ½ ) = 3/8
Probability of getting 2 heads = C(3,2)( ½ )( ½ )( ½ ) = 3/8
Thus, required probability = 1/8 + 3/8 + 3/8 = 7/8
Question: Two dice are thrown simultaneously. What is the probability of getting two numbers whose product is even?
Solution:
There might be 2 cases: both numbers are even or one is even and the other is odd.
Probability that both numbers are even = (3/6) (3/6) = ¼
Probability that one is even and the other is odd = (3/6) (3/6) x 2 = ½
Probability of getting 2 numbers whose product is even = ¼ + ½ = ¾
Tip #3: Probability of occurrence of mutually dependent or independent events is the product of their individual probabilities
Question: Two cards are drawn together from a pack of 52 cards. What is the probability that one is a spade and one is a heart?
Solution:
Probability of getting a Spade = 13 / 52 = ¼
Now, probability of getting a Heart = 13/51
Since the order of getting the cards is not mentioned, both the orders count.
Probability of getting a Spade and a Heart = 2 x (¼)(13/51) = 13 / 102
Question: A bag contains 4 white, 5 red and 6 blue balls. Three balls are drawn at random from the bag. Find the probability that all of them are red.
Solution:
Total no. of balls = 4+5+6 = 15
Probability of drawing a red ball at 1st draw = 5/15 = 1/3
Probability of drawing a red ball at 2nd draw = 4/14 = 2/7
Probability of drawing a red ball at 3rd draw = 3/13
Probability of drawing all 3 red cards = 1/3 x 2/7 x 3/13 = 2/91