| 1. |
Two taps A and B, when opened together, can fill a tank in 6 hours. How long will it take for the pipe A alone to fill the tank? I. B alone takes 5 hours more than A to fill the tank. II.The ratio of the time taken by A to that taken by B to fill the tank is 2 : 3. |
||||||||||||||||||||||||||||||||||||||||||
Answer: Option C Explanation: (A + B)'s 1 hour filling work = 1/6. I. Suppose A takes x hours to fill the tank. Then, B takes (X + 5) hours to fill the tank. 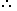 (A's 1 hour work) +(B's 1 hour work) (A's 1 hour work) +(B's 1 hour work)= (A + B)'s 1 hour work.
So, A alone takes 10 hours to fill the tank. II. Suppose A takes 2x hours and B takes 3x hours to fill the tank. Then,
Thus, each one of I and II gives the answer.
|
Each of the questions given below consists of a statement and / or a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statement(s) is / are sufficient to answer the given question. Read the both statements and
Give answer (A) if the data in Statement I alone are sufficient to answer the question, while the data in Statement II alone are not sufficient to answer the question.
Give answer (B) if the data in Statement II alone are sufficient to answer the question, while the data in Statement I alone are not sufficient to answer the question.
Give answer (C) if the data either in Statement I or in Statement II alone are sufficient to answer the question.
Give answer (D) if the data even in both Statements I and II together are not sufficient to answer the question.
Give answer(E) if the data in both Statements I and II together are necessary to answer the question.
Post your comments here:
Name *:
Email : (optional)
Your comments will be displayed only after manual approval.
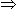

 1/ x =
1/ x =