Height and Distance


It is an important application of trigonometry which helps us to find the height of any object and distance of that object from any point which are not directly measurable. If the angle of elevation/depression from a point is known.

Line of Sight

A line of sight is the line drawn from the eye of an observer to the point, where the object is viewed by the observer.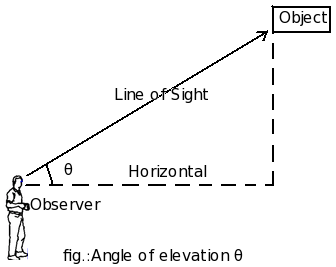

               


In this diagram,  marks the angle of elevation of the top of the object as seen from a point on the ground.

Horizontal Line

The line of sight which is parallel to ground level is known as horizontal line.

Angle of Elevation

The angle of elevation of the point viewed is the angle formed by the line of sight with the horizontal, when the point being viewed is above the horizontal level.

               


As shown in the diagram above, an observer is looking at an object located above the horizontal axis. In this process, it makes an angle with the x-axis. This angle is called angle of elevation.

Understanding the angle of elevation formula:

The angle of elevation formula helps to solve the angle of elevation problems very easily. As it is visible from the figure, the vertical from object makes an right angle with the horizontal. So if we know the height of the object and the linear distance, we can easily find out the angle by trigonometric formula. It is given by tan = Height / distance. The angle of elevation of the sun that is better known as altitude angle, can also be found by the same method.

Angle of Depression

When the line of sight is below the horizontal level, the angle so formed by the line of sight with the horizontal is called the angle of depression.

               


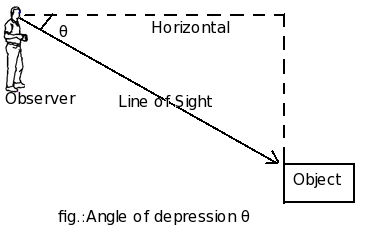
As shown, an observer is looking at the downwards object while making an angle with the horizontal axis. Here can be called the angles of depression for an observer.

MIND IT !

The angle of depression formula will provide an easy yet effective way for solving angle of depression problems. As it is clear from the picture, the vertical drawn upwards from the object makes an right angle with the horizontal. In that case, knowing the depth of the target object and the horizontal distance is enough to find the angle . A trig formula is required in this case. We know that tangent of an angle is equal to the ratio of the opposite side to adjacent. Applying this concept, tan = Height / distance. The same formula holds true for finding the angle of elevation also.

IMPORTANT FACTS AND FORMULAE

1. Trigonometry:

In a right angled OAB, where BOA = ,

               

i.   sin = Perpendicular = AB ;
Hypotenuse OB

ii.   cos = Base = OA ;
Hypotenuse OB

iii.  tan = Perpendicular = AB ;
Base OA

iv.  cosec = 1 = OB ;
sin AB

v.   sec = 1 = OB ;
cos OA

vi.  cot = 1 = OA ;
tan AB

2. Trigonometrical Identities:

  1. sin2 + cos2 = 1.

  2. 1 + tan2 = sec2 .

  3. 1 + cot2 = cosec2 .

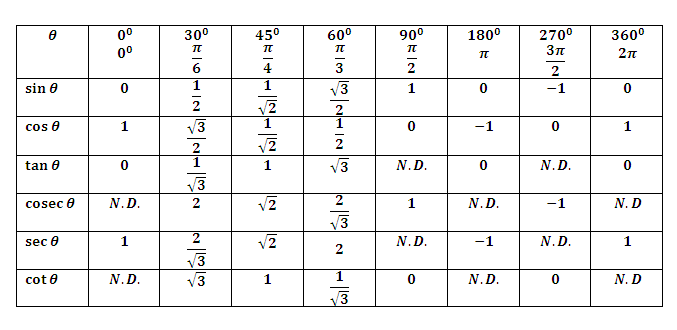
3. Values of T-ratios: