Compound Interest
As we know that when we borrow some money from bank or any person, then we have to pay some extra money at the time of repaying. This extra money is known as interest. If interest accrued on principal, it is known as simple interest.
Sometimes it happens that we repay the borrow money some late. After the completion of specific period, interest accrued on principal as well as interest due of the principal.
Then, it is known as compound interest.
Compound interest = Amount - Principal
Basic Formula Related to Compound Interest
Let Principal = P, Rate = R% per annum, Time = n years.
1. If interest is compound annually, then:
| Amount = P |  |
1 + | R |  |
n |
| 100 |
Compound interest = Amount - Principal
| Compound interest |
|
2. If interest is compounded half-yearly, then R = R/2 and n = 2n
| Amount = P | 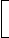 |
1 + | (R/2) | 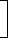 |
2n |
| 100 |
3. If interest is compounded quarterly, then R = R/4 and n = 4n
| Amount = P | 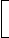 |
1 + | (R/4) | 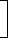 |
4n |
| 100 |
4. If interest is compounded annually but time is in fraction, (Suppose time = 3 years), then :
years), then :
| Amount = P |  |
1 + | R |  |
3 | x | 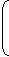 |
1 + |  R R |
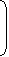 |
| 100 | 100 |
5. When Rates are different for different years, say R1%, R2%, R3% for 1st, 2nd and 3rd year respectively.
| Then, Amount = P |  |
1 + | R1 |  |
 |
1 + | R2 |  |
 |
1 + | R3 |  |
. |
| 100 | 100 | 100 |
TIPS on cracking Aptitude Questions on Compound Interest
Tip #1:Understand the formulae
1. Amount to be repaid after N years if simple interest is applied = P + (P x N x R) = P (1 + N x R)
2. Simple Interest = P x N x R
3. Amount to be repaid after N years if interest is compounded = P [(1 + R)^N]
4. Compound Interest = [P x (1 + R)^N] - P
Question: Simple interest on a certain sum of money for 3 years at 8% per annum is half the compound interest on Rs.4000 for 2 years at 10% per annum. Calculate the principal placed on simple interest.
Solution:
Let the Principal be Rs. P
Then, SI = (P x R x T) = 0.24P
Given CI = 4000(1 + 0.1)2 – 4000 = 4000(1.21 – 1) =4000 x 0.21
According to the question,
0.24P = 2000 x 0.21
=> P = 2000 x 0.21 / 0.24 = 2000 x 7 / 8 = Rs. 1750
Tip #2:If the interest rate is applied on a half-yearly, quarterly or monthly basis, the effective annual rate is calculated by compounding the interest
Question: What is the effective annual rate of interest corresponding to a nominal rate of 6% per annum payable half-yearly?
Solution:
Let the Principal be Rs. P.
Now, the rate is 6% per annum but the interest has to be paid twice a year (i.e.) an interest of 3% is applied every 6 months.
Amount to be repaid after 1 year = P x 1.03 x 1.03 = 1.0609P
=> Effective Annual Rate of interest = 6.09%
Tip #3:Use logarithms to find the time when compound rates are applied
1. log 2 = 0.301
2. log 3 = 0.477
3. log 4 = 0.602
4. log 5 = 0.699
5. log 6 = 0.778
6. log 7 = 0.845
Question: At 3% annual interest compounded monthly, how long will it take to double your money?
Solution:
Let the number of months be n and the Principal be Rs. P.
Then, P(1 + 0.03)n = 2P
=> (1 + 0.03)n = 2
=> n log ( 1.03) = log 2
=> n = log 2 / log 1.03 = 0.301 / 0.128 = 23.5
Thus. It’ll take 1 year and 11.5 months.

