Clock
A clock is an instrument which displays time divided into hours, minutes and seconds.
A clock mainly consists of four components.
Dial
A clock is a circular dial. The periphery of the dial is numbered 1 through 12 indicating the hours in a 12 h cycle.
The circumference of a dial is divided into 60 equal spaces called minute space or 12 equal spaces called hour spaces.
Every clock has mainly two hands, one is smaller and other is bigger. The smaller hand is slower the and the bigger hand is faster.
1. Minute Spaces:
The face or dial of watch is a circle whose circumference is divided into 60 equal parts, called minute spaces.
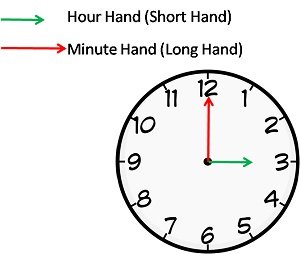
2. Hour Hand and Minute Hand:
A clock has two hands; the smaller one is called the hour hand or short hand while the larger one is called minute hand or long hand.
3. Second Hand:
Second hand indicates seconds on circular dial. It makes one revolution per minute.
Note : In 1 h minute hand covers 60 min spaces whereas the hour hand cover 5 min spaces.
Therefore, minute hand gains (60 -5) = 55 min in 1 h.
Important Points Related to Clock:
i. In 60 minutes, the minute hand gains 55 minutes on the hour on the hour hand.
ii. In every hour, both the hands coincide once. (i.e., 0° apart)
For example
Between 11 and 1'o clock, hands are together as shown in adjacent figure.

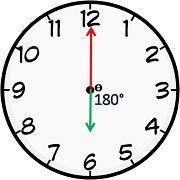
iii. The hands are in the same straight line when they are coincident or opposite to each other.
i.e., If two hands are in opposite direction. (180° apart), then they are 30 min spaces apart. This happens once in 1 h. In a period of 12 h both hands are in opposite direction 11 times and in a day both hands are in opposite direction 22 times.
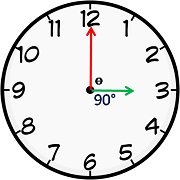
iv. When the two hands are at right angles, they are 15 minute spaces apart.
This happens twice in 1 h. In a period of 12 h, the hands are at right angle 22 times (2 common positions) and in a day both hands are at right angle 44 times.
v. When the hands are in opposite directions, they are 30 minute spaces apart.
vi. Angle traced by hour hand in 12 hrs = 360°
vii. Angle traced by minute hand in 60 min. = 360°.
viii. If a watch or a clock indicates 8.15, when the correct time is 8, it is said to be 15 minutes too fast.
On the other hand, if it indicates 7.45, when the correct time is 8, it is said to be 15 minutes too slow.
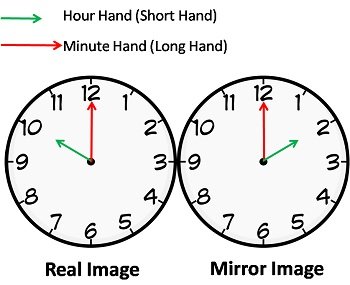
ix. If the real time is given and its MIRROR image is asked or vice – versa, simply subtract the given time from 11:60.
For example the time is 10:10 in the mirror then subtracting it from 11:60 we get 1:50 which will be the mirror image of the clock.
This is a very useful and time saving shortcut for exam and is rarely available in the section which increases its importance
x. A broken clock is right twice a day. However, a clock which gains or loses a few minutes might not be right twice a day or even once a day. It would be right when it had gained / lost exactly 12 hours.
Concept of Slow or Fast Clocks
If a watch/clock indicates 9 : 15, when the correct time is 9, then it is said to be 15 min too fast. On the other hand, if the watch/clock indicates 6 : 45, when the correct time is 7, then it is said to be 15 min too slow.
Example 1: What will be angle between the two hands of a clock at 9:50 ?
Solution: ∵ Angle traced by the hour hand in 12h = 3600
∴ Angle traced by the hour hand in 1 h = 3600/12
and angle traced by the hour hand in 9 h, 50 min
i.e., 59/6 h = (3600 x 50)/12 x 6 = 2950
Similarly,
∵ Angle traced by the minute hand in 60 min = 3600
∴ Angle traced by minute hand in 50 min = (3600 x 50)/60 = 3000
∴ Required angle = 3000 - 2950
Example 2: A clock gains 10 s in every 3 h. If the clock was set right at 4:00 am on Monday morning, then the time it will indicate on Tuesday evening at 7:00 pm.
Solution: Difference of time between 4:00 am on Monday to 7:00 pm Tuesday
24 + 12 + 3 = 39 h
Now, time gained by clock in 3 h = 10 s
Time gained by clock in 1 h = 10/3 s
∴ Time gained by clock in 39 h = (10 x 39)/3 = 130 s
=> Correct time is 7 : 02 : 10 pm.
TIPS on cracking Aptitude Questions on Clocks
Tip #1: Understand the basics of clock hand rotation
a) Angle covered by the second hand in 60 seconds = 360°
b) Angle covered by the second hand in 1 second = 6°
c) Angle covered by the minute hand in 60 minutes = 360°
d) Angle covered by the minute hand in 1 minute = 6°
e) Angle covered by the hour hand in 12 hours = 360°
f) Angle covered by the hour hand in 1 hour = 30°
g) Angle covered by the hour hand in 1 minute = 30°/60 = 1/2°
The minute and hour hands coincide 22 times in a day or 11 times in 12 hours. The timing of these coincidences are (approximately):

NOTE: Between 11 and 1, they coincide only once, i.e., at 12 o'clock
Tip #2: For problems on angles, draw diagrams to simplify the problem
Question: Calculate the reflex angle (greater angle) between the hands of a clock at 10:25.
Solution:
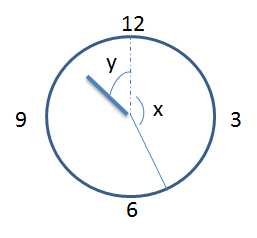
The minute hand moves 6° per minute => x = 25 x 6 = 150°
The hour hand moves 1/2° per minute.
At 1 hr 35 minutes to noon, y = 95 x ½ = 47.5°
Angle between the hands = x + y = 197.5°
Question: At what time between 7 and 8 o'clock will the hands of a clock be in the same straight line but, not together?
Solution:
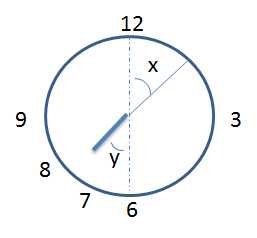
Let us assume that at m minutes past 7, the hands are at 180°
At m minutes past 7, x = y
The minute hand moves 6° per minute => x = m x 6
The hour hand moves 1/2° per minute => y = 30 + m x ½
m x 6 = 30 + m x ½
=> m = 60/11 minutes = 5 5/11 minutes
Tip #3: For problems on incorrect clocks, keep track of the correct time
Question: A watch which gains 5 seconds in 3 minutes was set right at 7 a.m. In the afternoon of the same day, when the watch indicated quarter past 4 o'clock, the true time is:
Solution:
The incorrect watch gains 5 seconds in 3 minutes, i.e., 100 seconds in 1 hour.
If 3600 seconds have elapsed, the incorrect watch will advance by 3700 seconds.
If 1 hr has elapsed, the incorrect watch will advance by 37/36 hrs.
Let the actual time elapsed be ‘t’ hrs. In time t, the watch will advance by 37/36 x t hrs.
From 7 a.m. till quarter past 4, the incorrect watch has advanced by 9.25 hrs = 37/4 hrs.
37/36 x t = 37/4 => t = 9 hrs => True time = 4 PM
Question: A watch gains 5 sec in 3 min and was set right at 8 AM. What time will it show at 10 PM on the same day?
Solution:
The incorrect watch gains 5 seconds in 3 minutes, i.e., 100 seconds in 1 hour.
From 8 AM to 10 PM on the same day, time passed = 14 hours.
=> In 14 hours, the incorrect watch would gain 1400 seconds = 23 minutes 20 seconds.
=> When the correct time is 10 PM, the incorrect watch would show 10: 23: 20 PM.
