Calendar
A calendar is chart or series of pages showing the days, weeks and months of a particular year. A calendar consist of 365 or 366 days divided into 12 months.
Important Points Related to Calendar
1. Ordinary Year:
The year which is not a leap year is called an ordinary years. An ordinary year has 365 days.
(52 complete weeks + 1 extra day = 365 days)
2. Leap Year:
A leap year has 366 days (the extra day is 29th of February) (52 complete weeks + 2 extra days = 366 days.)
(i). A leap year is divisible by 4 except for a century. For a century to be a leap year it must be divisible by 400.
(ii). Every 4th century is a leap year and no other century is a leap year.
Note: A leap year has 366 days.
Examples:
i. Years like 1988, 2008, 1676 are leap year (divisible by 4).
ii. Centuries like 2000, 2400 are leap year (divisible by 400).
iii. None of the years 2001, 2002, 2003, 2005, 2017 is a leap year (not divisible by 4).
iv. Centuries like 1700, 1800 are not leap year (not divisible by 400).
v. In a century, there is 76 ordinary year and 24 leap years.
3. Odd Days:
Extra days, apart from the complete weeks in a given period are called odd days. An ordinary year has 1 odd day while a leap year has 2 odd days.
To find the numbers of odd days
1. 1 ordinary year = 365 days = (52 x 7) + 1 = 52 weeks + 1 odd day.
1 ordinary year has 1 odd day.
2. Number of days in a leap year = 366 days = (52 weeks + 2 days)
A leap year has 2 odd days.
3. Number of days in a century (100 years)
= 76 ordinary years + 24 leap years
= (76 x 1 + 24 x 2) odd days = 124 odd days.
= (17 weeks + 5 days) 5 odd days.
Number of odd days in 100 years = 5.
MIND IT !
Number of odd days in 200 years = (5 x 2) 3 odd days.
Number of odd days in 300 years = (5 x 3) 1 odd day.
Number of odd days in 400 years = (5 x 4 + 1) 0 odd day.
Similarly, each one of 800 years, 1200 years, 1600 years, 2000 years etc. has 0 odd days.
4. Day of the Week Related to Odd Days:
| No. of days: | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Day: | Sun. | Mon. | Tues. | Wed. | Thurs. | Fri. | Sat. |
5. Day Gain/Loss
Ordinary Year (+/- 1 day)
i. When we proceed forward by 1 yr, then 1 day is gained.
For example: 9th August 2013 is Friday, then 9th August 2014 has to be Friday + 1 = Saturday.
ii. When we move backward by 1 yr, then 1 day is lost.
For example: 24th December 2013 is Tuesday, then 24th December 2012 has to be Tuesday - 1 = Monday
Leap Year (+/- 2 days)
i. When we proceed forward by 1 leap year, then 2 days are gained.
For example: If it is Wednesday on 25th December 2011, then it would be Friday on 25th December 2012 [Wednesday + 2] because 2012 is a leap year.
ii. When we move backward by 1 leap year, then 2 days are lost.
For example: If it is Wednesday on 18th December 2012, then it would be Monday on 18th December 20111. [Wednesday - 2] because 2012 is a leap year.
Exception
The day must have crossed 29th February for adding 2 days otherwise 1 day.
For example: If 26th January 2011 is Wednesday, 26th January 2012 would be Wednesday + 1 = Thursday (even if 2012 is a leap year, we have added + 1 day because 29 February is not crossed).
If 23rd March 20111 is Wednesday, then 23rd March 2012 would be Wednesday + 2 = Friday (+ 2 days 29th February of leap year is crossed).
TIPS on cracking Aptitude Questions on Calendars
Tip #1: Understand the basics of the Gregorian calendar
The day of the week repeats after every seven days.
For any time period, the no. of days in excess over complete weeks are called odd days.
A normal year has 365 days (i.e.) 52 weeks plus 1 odd day. When we proceed forward by one year, then 1 day is gained and vice-versa.
The number of days per month in a normal year are:

A year is considered to be a leap year if:
a) The year can be evenly divided by 4;
b) If the year can be evenly divided by 100, it is NOT a leap year, unless;
c) The year is also evenly divisible by 400. Then it is a leap year
Leap years have 366 days. The extra day is added to February which has 29 days in a leap year.
When we proceed forward by one leap year, then 2 odd days are gained because leap years have 366 days
Tip #2: If you have a reference day, then: Reqd. day= Ref. day ± N weeks ± M days
Question: What day of week was it on 5th November 1989 if it was Monday on 4th April 1988 ?
Solution:
4th April 1988 was a Monday.
1988 was a leap year, hence it has 2 odd days. However, since we are starting from April 4th, February has already been crossed and hence the extra odd day can be ignored.
=> 4th April 1989 was a Tuesday
No of days between 4th April 1989 and 5th November 1989
= 26 + 31+ 30 + 31 + 31 + 30 + 31 + 5 = 215 days (which has 5 odd days.)
5th November 1989 was a Sunday
Question: Find the year nearest to 2007 in future which is the same calendar year as it.
Solution:

When no. of odd days is multiple of 7, the year will have same calendar year as 2017.
In 2018, no. of odd days becomes 14. Thus, the reqd. year is 2018.
Note: The questions on calendars can be broadly categorized into 2 types:
1. Those that provide a reference day and need you to find the day of any particular date using the reference day.
2. Problems which do not provide any reference data but ask you to find the day of a particular date.
Although these might be complicated, there are some points and shortcuts that are helpful in solving the problems in just a few seconds.
If you have a reference day, express the required day in the form of
Required day = Reference day ± N weeks ± M days
Also, remember the following points:
a) The day of the week repeated after every seven days.
b) When we proceed forward by one year, then 1 day is gained and vice-versa.
c) When we proceed forward by one leap year, then 2 days are gained and vice-versa.
d) Every year divisible by 4 is a leap year, if it is not a century.
e) Every 4th century is a leap year and no other century is a leap year.
Tip #3: If you do not have a reference day, follow these 5 steps
First of all, memorize the following tables. Then follow the steps below.
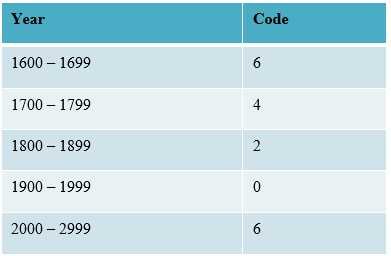
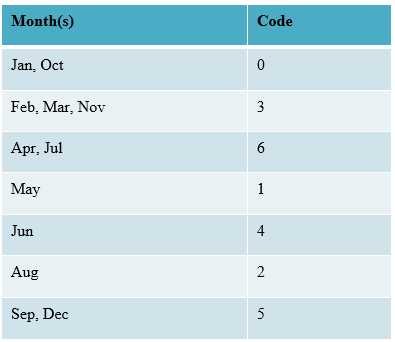
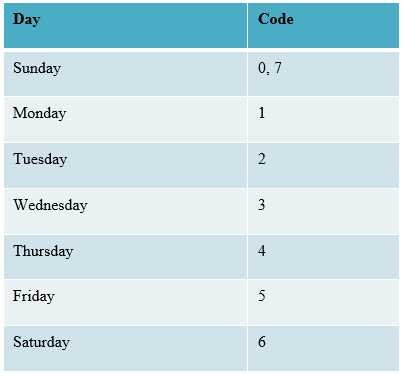
Step 1: Add the day digits to last two digits of the year.
Step 2: Divide the last two digits of the year by four and add it to the result in step 1.
Step 3: Add Month Code and year codes to the result obtain in step 3.
Step 4: Divide the result of step 4 by seven.
Step 5: Obtain the remainder and match with the day code.
Question: What was the day of the week on 17th June, 1998?
Solution:
Year Code: 0, Month Code: 4, Day digits = 17, Last 2 digits of the year = 98.
1. 17 + 98 = 115.
2. Quotient of 98 / 4 = 24, 115 + 24 = 139.
3. 139 + 4 + 0 = 143.
4. Remainder of 143 / 7 = 3.
5. Day code 3 = Wednesday.
Thus, 18th June 1998 was a Wednesday.
Question: Which days of the week cannot be the last day of a century?
Solution:
Year code = n, Month Code = 5, Day digits = 31, Last 2 digits of the year = 00, where n = 0, 2, 4 or 6.
1. 31 + 00 = 31.
2. Quotient of 00 / 4 = 0, 31 + 0 = 31.
3. 31 + 5 + n = 36 + n = 36, 38, 40 or 42.
4. Remainder of: 36 / 7 = 1, 38 / 7 = 3, 40 / 7 = 5, 42 / 7 = 0.
5. Day Code: 1 = Monday, 3 = Wednesday, 5 = Friday, 0 = Sunday.
Thus, the last day of a century cannot be Tuesday, Thursday or Saturday.
