Banker's Discount
IMPORTANT CONCEPTS
Banker's Discount:
Suppose a merchant A buys goods worth, say Rs. 10,000 from another merchant B at a credit of say 5 months. Then, B prepares a bill, called the bill of exchange. A signs this bill and allows B to withdraw the amount from his bank account after exactly 5 months.
The date exactly after 5 months is called nominally due date. Three days (known as grace days) are added to it get a date, known as legally due date.
Suppose B wants to have the money before the legally due date. Then he can have the money from the banker or a broker, who deducts S.I. on the face vale (i.e., Rs. 10,000 in this case) for the period from the date on which the bill was discounted (i.e., paid by the banker) and the legally due date. This amount is know as Banker's Discount (B.D.).
Thus, B.D. is the S.I. on the face value for the period from the date on which the bill was discounted and the legally due date.
Banker's Gain (B.G.) = (B.D.) - (T.D.) for the unexpired time.
Note: When the date of the bill is not given, grace days are not to be added.
IMPORTANT FORMULAE
Let F = Face Value of the Bill, TD = True Discount, BD = Bankers Discount, BG = Banker’s Gain, R = Rate of Interest, PW = True Present Worth and T = Time in Years
1. B.D. = S.I. on bill for unexpired time.
| 2. B.G. = (B.D.) - (T.D.) = S.I. on T.D. = | (T.D.)2 |
| P.W. |
3. T.D. = P.W. x B.G.
| 4. B.D. = | 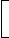 |
Amount x Rate x Time | 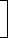 |
| 100 |
| 5. T.D. = | 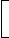 |
Amount x Rate x Time | 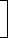 |
| 100 + (Rate x Time) |
| 6. Amount = | 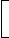 |
B.D. x T.D. | 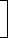 |
| B.D. - T.D. |
| 7. T.D. = | 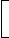 |
B.G. x 100 | 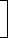 |
| Rate x Time |
TIPS on cracking Aptitude Questions on Bankers Discount
Tip #1: Understand the concepts in Banker’s Discount clearly
Scenario: Suppose A has borrowed Rs 1000 from B and this amount should be returned with interest after 1 year. Let us assume that the market interest rate is 5% per year [Simple Interest]. A hands over to B a note with a Face Value of Rs 1050, promising repayment after 1 year. [1000 + (1000 x 0.05 x 1yr) = 1050]
After 6 months, B decides that he needs the money immediately and cannot wait till the due date which is 6 months away. B approaches a bank and hands over the note from A with Face Value of Rs 1050 due after 6 months.
Calculating True Discount:
The present value (or true value) of the note from A is calculated as follows:
PV x (1 + r x t) = FV [Here, PV is the present value, r is the rate of simple interest, t is time and FV is the Face Value of the note.]
Present Value (or True Value) = 1050/(1.025) = Rs. 1024.4
True discount = Face Value – Present Value = 1050 – 1024.4 = Rs. 25.6
But, if the bank paid out Rs 1024.4 to B in exchange for the note, the bank would not make a profit. The bank does not use True Discount but uses another formula to calculate the discount called Banker’s Discount.
Calculating Banker’s Discount:
Banker’s Discount: The Simple Interest on the Face Value of the debt for the time period between the legally due date and the date on which the bill is discounted is called Banker’s Discount.
Banker’s Discount = FV x r x t = 1050 x 0.05 x (1/2) = Rs 26.25
Note:
True Discount = FV – [FV / (1 + r x t)] = FV [r x t / (1 + r x t)] < FV x r x t
=> True Discount < Banker’s Discount
Instead of discounting True Discount, the Bank discounts the Banker’s Discount from the Face Value and pays out Rs 1050 – 26.25 = Rs. 1023.75
Banker’s Gain = Present Value of the Note – Actual Payout
= (Face Value – True Discount) – (Face Value – Banker’s Discount)
= Banker’s Discount – True Discount [This figure is always positive]
Question: The banker's gain on a sum due 3 years hence at 12% per annum is Rs. 270. What is the banker’s discount?
Solution:
Banker’s Discount = FV x r x t = 0.36 x FV
True Discount = FV – PV = FV – FV / [1 + (r x t)] = FV – FV / 1.36
= 0.36 x FV / 1.36 = Banker’s Discount / 1.36
Banker’s Gain = Banker’s Discount – True Discount = BD - BD/1.36 = 270
=> Banker’s Discount, BD = 270 x 1.36 / 0.36 = Rs. 1020
Moving on, we come to the formulae in Banker’s Discounts.
Question: The banker's discount on a certain sum due 2 years hence is 11/10 of the true discount. What is the rate?
Solution:
BD = FV x r x t
TD = FV – PV = FV – FV / [1 + (r x t)] = FV x r x t / [1 + (r x t)]
BD/ TD = 1 + (r x t) = 11/10
2r = 1/10
=> r = 1/20 = 0.05 or 5%
Tip #2: For transactions that do not involve a bank, use True Value
Question: A man purchased a cow for Rs. 3000 and sold it the same day for Rs. 3600, allowing the buyer a credit of 2 years. If the rate of interest be 10% per annum, then what is his gain?
Solution:
Present Value = 3600/[1+(0.10 x 2)] = Rs 3000
Gain = Present Value – Cost = 0
Question: A trader owes a merchant Rs. 10,028 due 1 year hence. The trader wants to settle the account after 3 months. If the rate of interest 12% per annum, how much cash should he pay?
Solution:
Face Value = Rs. 10028, r = 12% p.a.
Present Value after 9 months = 10028/[1+(0.12*9/12)] = Rs 9200