Average
An average or an arithmetic mean of given data is the sum of the given observations divided by number of observations.
For example If we have to find out the average of 10, 15, 25 and 30, then the required average will be equal to
| 10 + 15 + 25 + 30 | = | 80 | = 20 | |
| 4 | 4 |
Therefore, we can write the formula
| Average (A) = | Sum of observations (S) | ||
| Number of observations (N) |
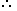 (A) = (A) = |
(S) | ||
| (N) |
Properties of Average
- Average of a given data is less than the greatest observation and greater than the smallest observation of the given data.
For example Average of 3, 7, 9 and 13
Required average = 3 + 7 + 9 + 13 = 32 = 8 4 4 Clearly, 8 is less than 13 and greater than 3.
- If the observations of given data are equal, then the average will also be the same as observations.
For example Average of 6, 6, 6 and 6 will be 6 because
Required average = 6 + 6 + 6 + 6 = 24 = 6 4 4 - If 0 (zero) is one of the observation of a given data, then that 0 (zero) will also be included while calculating average.
For example Average of 3, 6 and 0 is 3 because
Required average = 3 + 6 + 0 = 9 = 3 3 3
Note :
- If all the numbers get increased by a, then their average must be increased by a.
- If all the numbers get decreased by a, then their average must be decreased by a.
- If all the numbers are multiplied by a, then their average must be multiplied by a.
- If all the numbers are divided by a, then their average must be divided by a.
Important Formula Related to Average of Numbers
| 1. Average of first n natural numbers = |  |
n + 1 |  |
| 2 |
2. Average of first n even numbers = (n + 1)
3. Average of first n odd numbers = n
4. Average of consecutive numbers :
| A = |  |
First number + Last number |  |
| 2 |
5. Average of 1 to n odd numbers :
| A = |  |
Last odd number + 1 |  |
| 2 |
6. Average of 1 to n even numbers :
| A = |  |
Last even number + 2 |  |
| 2 |
7. Average of squares of first n natural numbers:
A = (n + 1) (2n + 1) 6
8. Average of the cubes of first n natural numbers:
A = n(n + 1) 2 4
9. Average of n multiples of any number:
A = Number x (n + 1) 2
Average Speed:
Average speed is defined as total distance travelled divided by total time taken.
| Average speed = | Total distance travelled | ||
| Total time taken |
Case #1: Suppose a man covers a certain distance at A kmph and an equal distance at B kmph.
Then, the average speed druing the whole journey is :
 |
2AB |  |
kmph. | |
| A + B |
Example - A person covers a certain distance by car at a speed of 25 km/h and comes back at a speed of 40 km/h. What is his average speed during his travel?
Sol. Here, A = 25km/h and B = 40 km/h
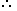 Required average speed = Required average speed = |
 |
2AB |  |
kmph. |
| A + B |
| = | 2 x 25 x 40 | = | 2000 | = 30.76 km/h |
| 25 + 40 | 65 |
Case #2: If a person covers three equal distances at the speed of A km/h, B km/h and C km/h respectively, then the average speed during the whole journey will be :
 |
3ABC |  |
kmph. | |
| AB + BC+CA |
Example - If a person covers three equal distances at the speed of 30 km/h, 15 km/h and 10 km/h respectively, then find out his average speed during the whole journey.
Sol. Here, A = 30 km/h, B = 15 km/h and C = 10 km/h
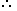 Required average speed = Required average speed = |
 |
3ABC |  |
kmph. |
| AB + BC+CA |
| = |  |
3 x 30 x 15 x10 |  |
kmph. |
| 30 x 15 + 15 x 10+10 x 30 |
| = | 3 x 30 x 15 x 10 | = | 3 x 30 x 15 x 10 | |
| 450 + 150 + 300 | 900 |
= 15 km/h
TIPS on cracking Aptitude Questions on Averages
Tip #1: If terms are in progression, the average is either the middle term or average of the two middle terms
Question 1: Find the average of first 5 multiples of 3.
Solution:
Number of terms= 5= odd.
Average= Middle term= 3rd term= 3x3= 9
Question 2: The heights of 6 students in a class are 5ft, 5.2ft, 5.4ft, 5.6ft, 5.8ft and 6ft respectively. What is their average height?
Solution:
Average= Average of middle terms = (5.4+5.6)/2 ft= 5.5ft.
Note: If the terms have a constant difference, the average will be given by:
a. The middle term if the number of terms is odd.
b. The average of the two middle or of the two extreme terms. Both will give the same result.
Tip #2: If a person travels same distances with different speeds, then the average speed is not the arithmetic mean but the harmonic mean
If a person covers a distance d first at x km/hr and then covers the same distance d at y km/hr, then the average speed is:
= Total distance travelled/ Total time taken
= 2d/ (d/x + d/y)
= 2d/ [(yd + xd)/xy]
= 2dxy/[d(x+y)]
= 2xy/ x+y (Harmonic mean of x and y)
Question: A travels 25km at 50 km/hr and then 25km again with 70km/hr. What is A’s average speed during the whole journey?
Solution:
Average speed for the whole journey
= (2x50x70) / (50+70)= 58.3km/hr
Tip #3: When dealing with problems where average changes by addition/ removal, create an equation of the form: New_total/New Count = Old_Total/Old Count (+/- Change in Average)
Question: The average weight of a class of 24 students is 35 kg. If the weight of the teacher be included, the average rises by 400 g. What is the weight of the teacher?
Solution:
(24 * 35 + Wteacher)/ 25 = 35 + 0.4
24 * 35 + Wteacher = 35 * 25 + 10
Wteacher = 35 + 10 = 45 kgs
Question: When a student weighing 45 kgs left a class, the average weight of the remaining 59 students increased by 200g. What is the average weight of the remaining 59 students?
Solution:
Wremaining_students / 59 = (Wremaining_students + 45) / 60 + 0.2
60 * Wremaining_students = (59 * Wremaining_students) + (59 * 45) + (59 *12)
Wremaining_students / 59 = 45 + 12 = 57 kgs
