Alligation or Mixture
Mixture
The new product obtained by mixing two or more ingredients in a certain ratio is called a mixture.
or
Combination of two or more quantities is known as mixture.
Important Facts and Formulae
1. Alligation:
It is the rule that enables us to find the ratio in which two or more ingredients at the given price must be mixed to produce a mixture of desired price.
2. Mean Price:
The cost of a unit quantity of the mixture is called the mean price. It will always be higher than cost price of cheaper quantity and lower than cost price of dearer quantity.
3. Rule of Alligation:
If two ingredients are mixed, then

We present as under:
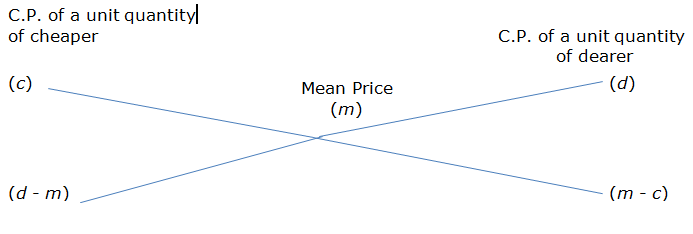
 (Cheaper quantity) : (Dearer quantity)
= (d - m) : (m - c).
(Cheaper quantity) : (Dearer quantity)
= (d - m) : (m - c).
MIND IT !
The rule is also applicable for solving questions based on average i.e., speed, percentage, price, ratio, etc., and not for absolute values. In other words, we can use this method whenever per cent, per hour, per kg etc., are being compared.
4. Suppose a container contains x of liquid from which y units are taken out and replaced by water.
After n operations,
the quantity of pure liquid =  units.
units.
TIPS on cracking Aptitude Questions on Alligation or Mixture
Tip #1: Volume of a substance in the final solution = Sum of volumes of the substance in the ingredients
Question: How many liters of pure alcohol must be added to a 100 liter solution that is 20% alcohol in order to produce a solution that is 25% alcohol?
Solution:
Here, let us add X liters of 100% alcohol to 100 liters of 20% alcohol to produce 25% alcohol. Then,
Volume of alcohol in the original 100 liter solution = 20% x 100 liters = 20 liters
Volume of alcohol in the pure alcohol solution = X liters
Total volume of alcohol in the final solution = 25% x (100 + X) liters
Volume of alcohol in the final solution = Sum of the volumes of alcohol in the two liquids being mixed
0.25 x (100 + X) liters = 20 + X liters
= X = 20 / 3 liters
Tip #2: From a solution of volume V containing x percent of a substance, if y liters are replaced by water, the new percentage of the substance in the solution = x (V-y)/ V
Question: 8 liters are drawn from a cask full of pure wine and is then filled with water. This operation is performed three more times. The ratio of the quantity of wine now left in cask to that of water is 16: 65. How much wine did the cask hold originally?
Solution:
Let Vw be the volume of wine in the cask originally.
Let Vt be the total volume of liquid in the cask.
Let X be the percentage of wine in the cask originally.
X = original volume of wine/ total volume of liquid in the cask = Vw / Vt
When 8 liters are drawn out, the volume of wine is reduced by 8 X liters while the total volume of liquid remains unchanged as it is re-filled with water.
Let X’ be the new percentage of wine in the cask after this operation
X’ = (original volume of wine – 8 X) / total volume of liquid in the cask
= [Vw – 8 (Vw/ Vt)] / Vt
= X (Vt – 8) / Vt
After 4 such replacement operations, X’’’’ = X [(Vt – 8)/ Vt] ^ 4
From the problem, X’’’’ = 16/ (16 + 65) = 16/ 81
Also, since originally the cask was full of pure wine, X = 1
[(Vt – 8)/ Vt] ^ 4 = 16/ 81
=> Vt = 24 liters
